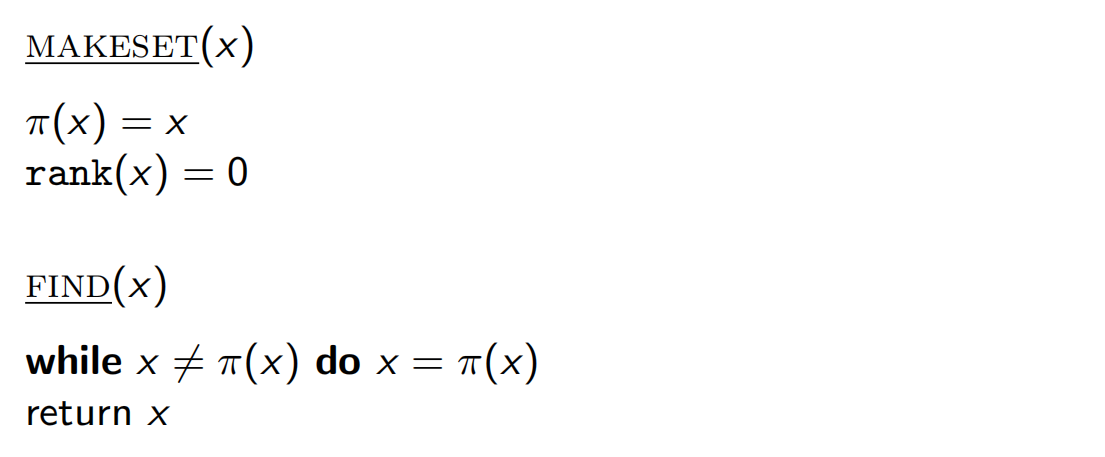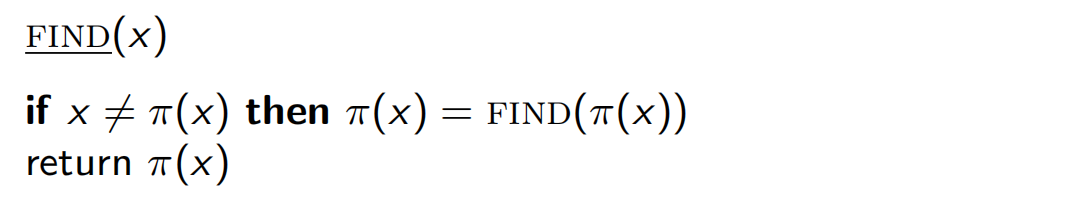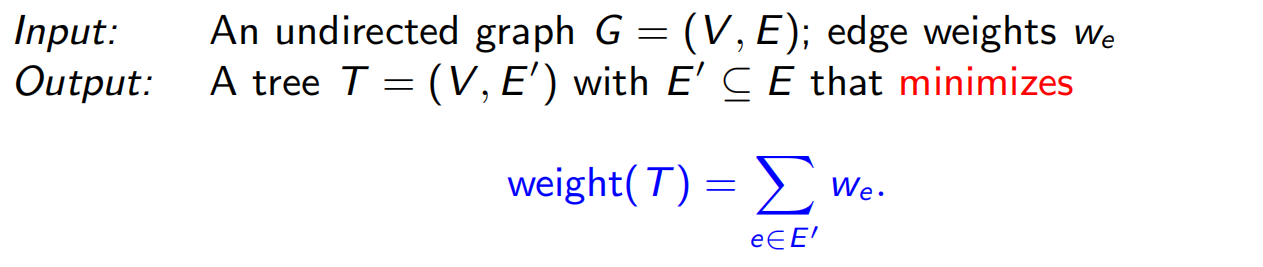数据结构总结

2025-05-29

学习

11k words

阅读次

——smiling

用于整理任老师Slides中出现的知识点。

已更新完毕。

15.5 平摊分析

略。

16 栈

先进后出

进栈出栈都是在栈顶操作

顺序（数组尾部作为栈顶）实现/链接（单链表）实现

STL中的栈：stack，默认实现方式为deque

函数：

create()：创建一个空的栈；
进栈push(x)：将x插入栈中，使之成为栈顶元素；
出栈pop()：删除栈顶元素并返回栈顶元素值；注：有些实现中pop不返回栈顶元素，如stl
读栈顶元素top()：返回栈顶元素值但不删除栈顶元素
判栈空isEmpty()：若栈为空，返回true，否则返回false。

栈的应用：

递归函数的非递归实现

设置一个栈：
    记录要做的工作，即要排序的数据段
栈元素的格式：
    struct node{
        int left;
        int right;
    };
先将整个数组进栈，然后重复下列工作，直到栈空：
    从栈中弹出一个元素，即一个排序区间
    将排序区间分成两半
    检查每一半，如果多于一个元素，则进栈

void quicksort( int a[], int size){
    seqStack <node> st;
    int mid, start, finish;
    node s;
    if (size <= 1) 
        return;
    s.left = 0;
    s.right = size - 1;
    st.push(s);
    while (!st.isEmpty()) {
        s = st.pop();
        start = s.left;
        finish = s.right;
        mid = divide(a, start, finish);
        if (mid - start > 1) {
            s.left = start;
            s.right = mid - 1;
            st.push(s);
        }
        if (finish - mid > 1) {
            s.left = mid + 1;
            s.right = finish;
            st.push(s)；
        }
    }
}

int divide(int a[], int start, int finish) {
    int pivot = a[finish];
    int i = start - 1;
    
    for (int j = start; j < finish; j++) {
        if (a[j] <= pivot) {
            i++;
            std::swap(a[i], a[j]);
        }
    }
    
    std::swap(a[i + 1], a[finish]);
    return i + 1;
}

符号平衡检查

要考虑的特殊情况：

1.字符串常量和字符常量中的括号不用考虑，注释中的括号不用考虑，C++中的注释又有两种形式：以“//”开始到本行结束，以“/*”开始到“*/”结束，可以跨行

2.读文件，直到读到一个和参数值相同的符号。几个特殊情况：

字符或字符串常量是不允许跨行的。如果在读文件的过程中遇到了回车或文件结束，则输出出错信息。

在字符或字符串常量中可能会包含单引号或双引号，此时不能将这个单引号或双引号作为结束符。如何知道这个单引号或双引号代表的是普通的字符而不是结束符呢？C++采用了转义字符来表示，因此当读到一个表示转义字符开始的标记（\）时，不管它后面是什么符号，都不用检查。

表达式的计算

将中缀表达式转换为后缀表达式

后缀表达式：遇到运算符，将前面离它最近的两个运算数进行运算，不需要括号，不考虑优先级和结合性

计算后缀表达式利用栈。

只包含加、减、乘、除运算以及括号
遍历中缀表达式
	若读入的是操作数，立即输出。
	若读入的是闭括号，则将栈中的运算符依次出栈并输出，直到遇到相应的开括号，将开括号出栈。
	若读入的是开括号，则进栈。
	若读入的是运算符，如果栈顶运算符优先级高于或等于（左结合）读入的运算符，则栈顶运算符出栈；直到栈顶运算符优先级低于读入的运算符为止，读入的运算符进栈。
在读入操作结束时，将栈中所有的剩余运算符依次出栈并输出，直至栈空为止。

两个操作可以合并：发现某个运算符可以出栈时，则直接执行运算

伪代码：

int calc::result(){
    token lastOp, topOp;
    int result_value, CurrentValue;
    seqStack<token> opStack; //运算符栈
    seqStack<int> dataStack; //运算数栈
    char *str = expression; //为什么引进str
    while (true){
        lastOp = getOp(CurrentValue); //读取表达式
        if (lastOp == EOL) break;
        switch (lastOp) {
            case VALUE: dataStack.push(CurrentValue) ; break;
            case CPAREN: //进行括号内的运算
                while( !opStack.isEmpty() && (topOp = opStack.pop()) != OPAREN ) 
                    BinaryOp(topOp, dataStack);
                if ( topOp != OPAREN) 
                    cerr << "缺左括号!" << endl;
                break;
            case OPAREN: case EXP: opStack.push(lastOp); break;
            case MULTI:case DIV:
                while ( !opStack.isEmpty() && opStack.top() >= MULTI) 
                    BinaryOp(opStack.pop(), dataStack);
                opStack.push(lastOp); 
                break;
            case ADD:case SUB:
                while ( !opStack.isEmpty() && opStack.top() != OPAREN ) 
                    BinaryOp(opStack.pop(), dataStack );
                opStack.push(lastOp);
        }
    }
    while (!opStack.isEmpty())
        BinaryOp(opStack.pop(),dataStack);
    if (dataStack.isEmpty()) {
        cout << "无结果\n";
        return 0;
    }
    result_value = dataStack.pop();
    if (!dataStack.isEmpty()) {
        cout << "缺操作符";
        return 0;
    }
    expression = str;
    return result_value ;
}
void calc::BinaryOp( token op, seqStack<int> &dataStack){
    int num1, num2;
    if ( dataStack.isEmpty()) { cerr << "缺操作数! "; exit(1); }
    else num2 = dataStack.pop();
    if ( dataStack.isEmpty()) { cerr << "缺操作数! "; exit(1); }
    else num1 = dataStack.pop();
    switch(op) { //执行运算并将结果入栈
        case ADD: dataStack.push(num1 + num2); break;
        case SUB: dataStack.push(num1 - num2); break;
        case MULTI: dataStack.push(num1 * num2); break;
        case DIV: dataStack.push(num1 / num2); break;
        case EXP: dataStack.push(pow(num1,num2));
    }
}

17 队列

先进先出

queue

顺序（队头位置固定/队头位置不固定/循环队列）实现 / 链接（单链表）实现

pop()移出头部元素但不返回此元素，需要通过front()先获取

STL中的队列类是一个容器适配器

可以借助的容器有list和deque(双向开口的分段连续线性空间，利用一块map空间，其中每个元素是一个指针，指向一块缓冲区)，缺省为deque 。

STL中队列的运算：

入队操作push：调用push_back
出队操作pop：调用pop_front
获得队头元素的操作front
获得队尾元素的函数back
判队列为空的函数empty
获得队列长度的函数size

队列的应用：

列车车厢重排

利用k根轨道重排n节车厢，初始排列次序在数组in中
缓冲轨是先进先出，所以每条轨道用一个队列模拟
处理过程：依次取入轨的队头元素，直到队列为空
	进入一条最合适的缓冲轨道
	检查每条缓冲轨道的队头元素，将可以放入出轨的元素出队，进入出轨
    
关键问题：合适的轨道
基本要求：
	轨道上最后一节车厢的编号小于进入的车厢编号
    没有满足基本要求的轨道，则启用一条新轨道
最优要求：
	满足基本要求的轨道中最后一节车厢编号最大者
	例如处理车厢8，现有轨道情况
	轨道1: 2、5
	轨道2：3、7
	8应该放入轨道2。如果放入轨道1，假如后面一节车厢是6号，则必须启用一根新的轨道
在队列类中增加一个getTail的函数

排队系统的模拟

totalWaitTime = 0;
设置顾客开始到达的时间currentTime = 0;
for (i=0; i<customNum; ++i) {
    生成下一顾客到达的间隔时间；
    下一顾客的到达时间currentTime += 下一顾客到达的间隔时间；
    将下一顾客的到达时间入队；
}
从时刻0开始模拟;
while （顾客队列非空）{
    取队头顾客；
    if （到达时间 > 当前时间）
        直接将时钟拨到事件发生的时间；
    else 收集该顾客的等待时间；
    生成服务时间；
    将时钟拨到服务完成的时刻；
}
返回平均等待时间=等待时间/顾客数；

用两个栈实现队列，分析操作的时间复杂性

入队：进栈S1，O(1)

出队：将栈S2栈顶元素出栈，如果S2为空，则将S1中的元素依次出栈S1并进入S2直至S1为空。单次操作最好情况O(1)，最坏O(n)，由于每个元素仅会从S1到S2一次，因此平摊成本为O(1)

17.5 哈希

通用哈希函数族：对于任意两个不同的数据x和y，函数族H中恰有|H|/n个哈希函数将x和y映射到同一个目标值，n为可能的不同目标值数量

即对于任意的两个数据，如果哈希函数随机从一个通用哈希函数族选取，则冲突概率为1/n

哈希碰撞的解决方法：

闭散列表：利用本散列表中的空余单元

线性探测法：当散列发生冲突时，探测下一个单元，直到发现一个空单元。采用迟删除：找到该元素，做一个删除标记。

int (*key)(const KEY &x); //指向函数的指针，该函数将关键字转换为整型数
//函数指针定义格式：返回类型 （*指针变量)(形参表)
closeHashTable<Type>::closeHashTable (int length, int (*f)(const Type &x) ){
    size = length;
    array = new node[size];
    key = f;
}

二次探测法：当发生冲突时，下一个探测的单元是 $(k+1 )^2 , ( k+2)^2 , (k+3)^2 , \cdots$
再次散列法：采用第二个散列函数

开散列表：将碰撞的节点组成一个线性表，碰撞元素个数变化很大，所以用链表存储

STL中的无序关联容器：unordered_map，unordered_multimap，unordered_set，unordered_multiset

unordered_map：底层的实现是一个hash表+链表（处理冲突）实现的，所以数据的组织形式是无序的。unordered_map 特点就是搜寻效率高，时间复杂度为常数级别O(1)，而额外空间复杂度则要比较高

习题：

给定一个包含 0 和 1 的二进制数组，找到具有相同数量的 0 和 1 的最大子数组。

Input: { 0, 0, 1, 0, 1, 0, 0 }，Output: { 0, 1, 0, 1 } or { 1, 0, 1, 0 }

将 0 替换为 -1 并找出总和为 0 的最大子数组。

如果[ai,…,aj]为总和为0的子数组，则[a0 ,…,ai-1 ]的总和与[a0 ,…,aj]相同

18 字符串

顺序实现：略

链表实现：块状链表+插入删除子串的时候先分裂再插入再合并

串匹配

KMP算法

oiwiki

vector<int> prefix_function(string s) {
    int n = (int)s.length();
    vector<int> pi(n);
    for (int i = 1; i < n; i++) {
        int j = pi[i - 1];
        while (j > 0 && s[i] != s[j]) j = pi[j - 1];
        if (s[i] == s[j]) j++;
        pi[i] = j;
    }
    return pi;
}//pi：前缀函数

vector<int> find_occurrences(string text, string pattern) {
    string cur = pattern + '#' + text;
    int sz1 = text.size(), sz2 = pattern.size();
    vector<int> v;
    vector<int> lps = prefix_function(cur);
    for (int i = sz2 + 1; i <= sz1 + sz2; i++) {
        if (lps[i] == sz2) v.push_back(i - 2 * sz2);
    }
    return v;
}//KMP查找子串

BM算法

oiwiki

（说实话没太看懂…要是有考到过再复习吧）

回文串 - Manacher算法

oiwiki

以及B站上面一个个人认为讲得比较清楚的视频：

s[0] = '$'; s[++m] = '#';
for (b = 1; ss[b] != '\0'; ++b) {
    s[++m] = ss[b];
    s[++m] = '#';
}
s[++m] = '?';
for (int i = 1; i < m; ++i) {
    if (maxid > i) p[i] = min(maxid-i, p[2*id-i]);
    else p[i] = 1;
    while (s[i-p[i]] == s[i+p[i]]) p[i]++;
    if (i + p[i] > maxid) {
        maxid = i + p[i];
        id = i;
    }
}

19 树

二叉树

优美程度：二叉树<完全二叉树（最后一层必须从左到右填）<满二叉树（所有层刚好填满）

二叉树的性质：

完全二叉树可以按下面的方式编号，如果是普通二叉树则需要用特殊的值代表假节点

1 2	#define ls (p << 1) #define rs (p << 1 \| 1)

二叉树的遍历：

前序（根->左子树->右子树）、中序（左子树->根->右子树）、后序（左子树->右子树->根）、层次遍历

前序 + 中序可以唯一确定一棵二叉树

前序: A、B、D、E、F、C，中序: D、B、E、F、A、C

由前序找出根节点，通过根节点在中序中区分左右子树，继续对左右子树重复以上过程

由二叉树的后序序列和中序序列同样可以唯一地确定一棵二叉树

但是，已知二叉树的前序遍历序列和后序遍历序列却无法确定一棵二叉树。

前序便历非递归实现：从栈中取出一个节点，输出根节点的值；然后把右子树，左子树放入栈中

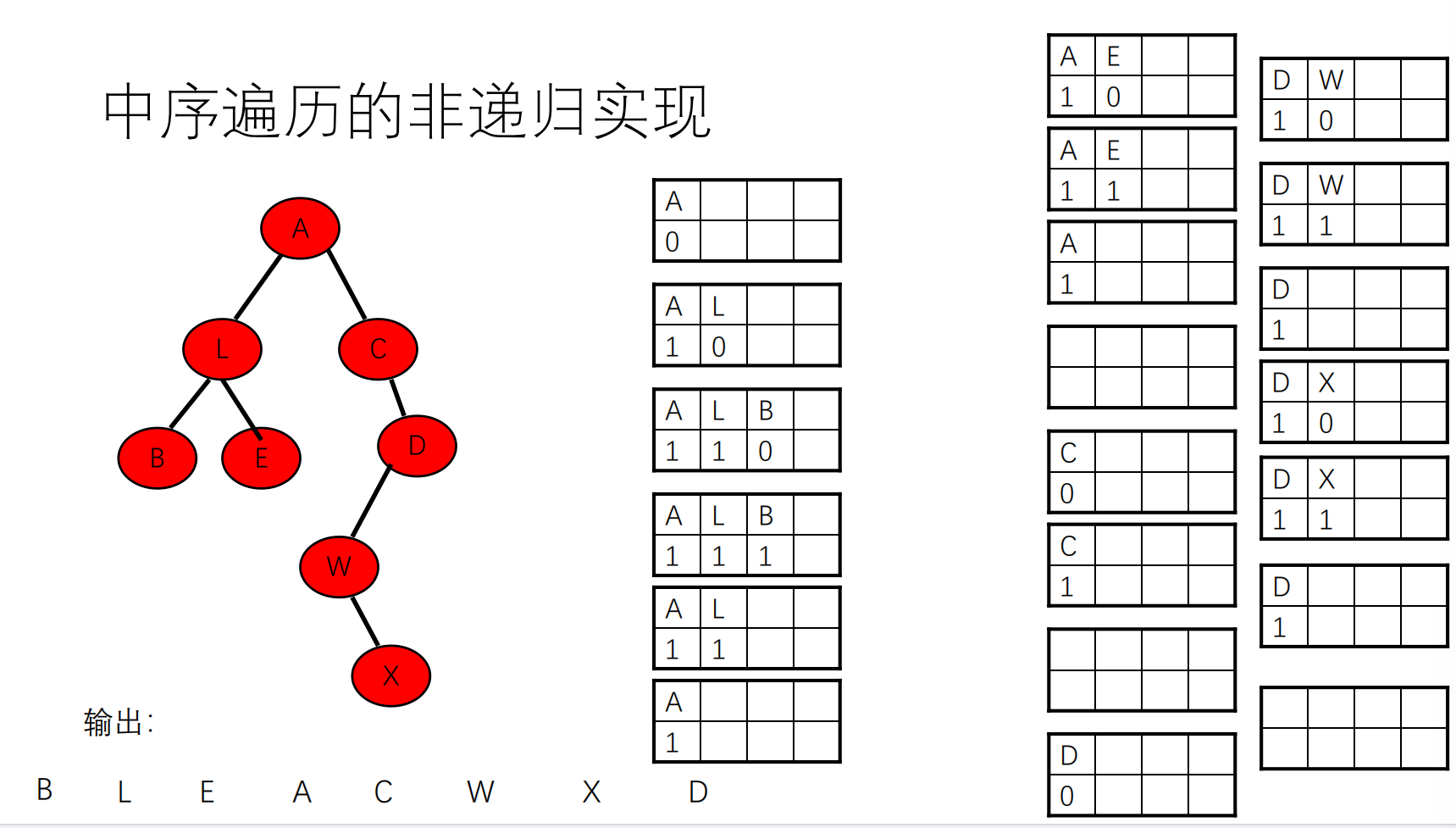
中序遍历非递归实现：当根节点出栈时，不能访问它，而要访问它的左子树。仍可以把它存在栈中，接着左子树也进栈。此时执行出栈操作，出栈的是左子树。左子树访问结束后，再次出栈的是根节点，此时根节点可被访问。根节点访问后，访问右子树，则将右子树进栈。

template <class Type>
    void BinaryTree<Type>::midOrder() const{
        linkStack<StNode> s;
        StNode current(root);
        cout << "中序遍历: ";
        s.push(current);
        while (!s.isEmpty()) {
            current = s.pop();
            if ( ++current.TimesPop == 2 ) {
                cout << current.node->data;
                if ( current.node->right != nullptr ) 
                    s.push(StNode(current.node->right ));
            }
            else { 
                s.push( current );
                  if ( current.node->left != nullptr ) 
                      s.push(StNode(current.node->left) );
                 }
        }
    }

后序遍历非递归实现：将中序遍历的非递归实现的思想进一步延伸

将树根进栈
出栈，直到栈为空
	第一次出栈，不能访问，应该访问左子树。于是，根节点重新入栈，并将左子树也入栈。
	第二次出栈，还是不能访问，要先访问右子树。于是，根节点再次入栈，右子树也入栈。
	第三次出栈，访问节点

template <class Type>
    void BinaryTree<Type>::postOrder() const{
        linkStack< StNode > s; StNode current(root);
        cout << "后序遍历: ";
        s.push(current);
        while (!s.isEmpty()) {
            current = s.pop();
            if ( ++current.TimesPop == 3 ) { 
                cout << current.node->data; 
                continue; 
            }
            s.push( current );
            if ( current.TimesPop == 1 ) {
                if ( current.node->left != nullptr ) 
                    s.push(StNode( current.node->left) );
            }
            else {
                if ( current.node ->right != nullptr ) 
                    s.push(StNode( current.node->right ) );
            }
        }
    }

顺序实现与链接实现

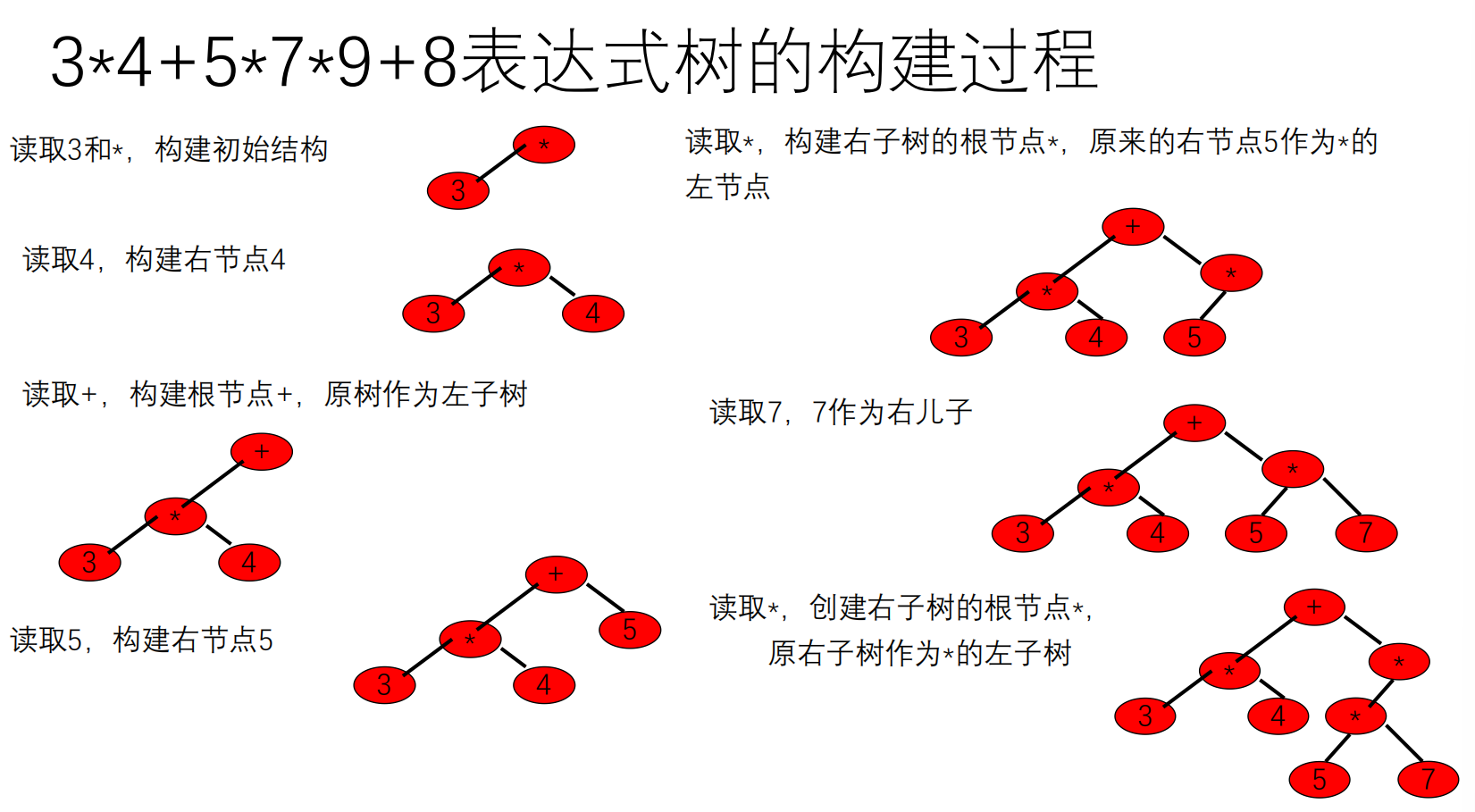
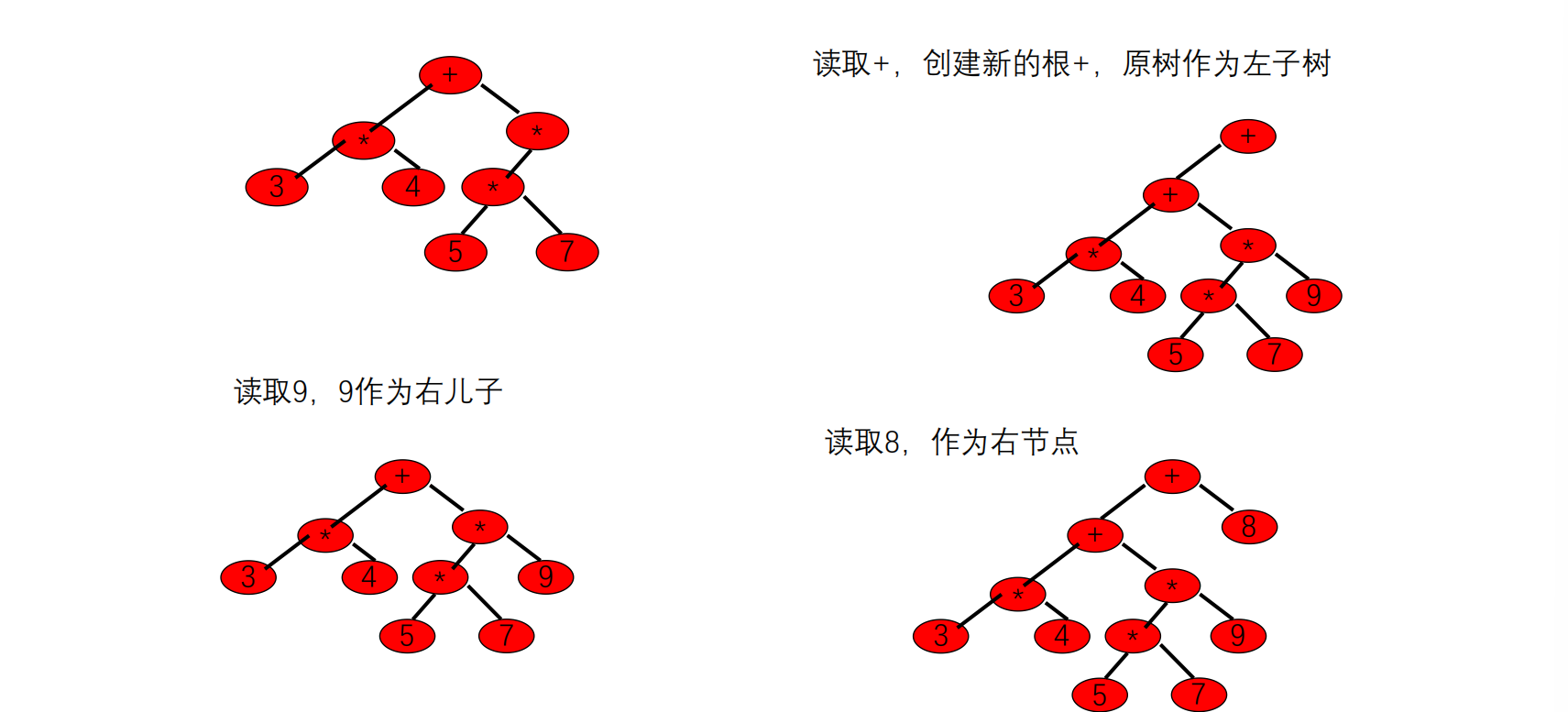
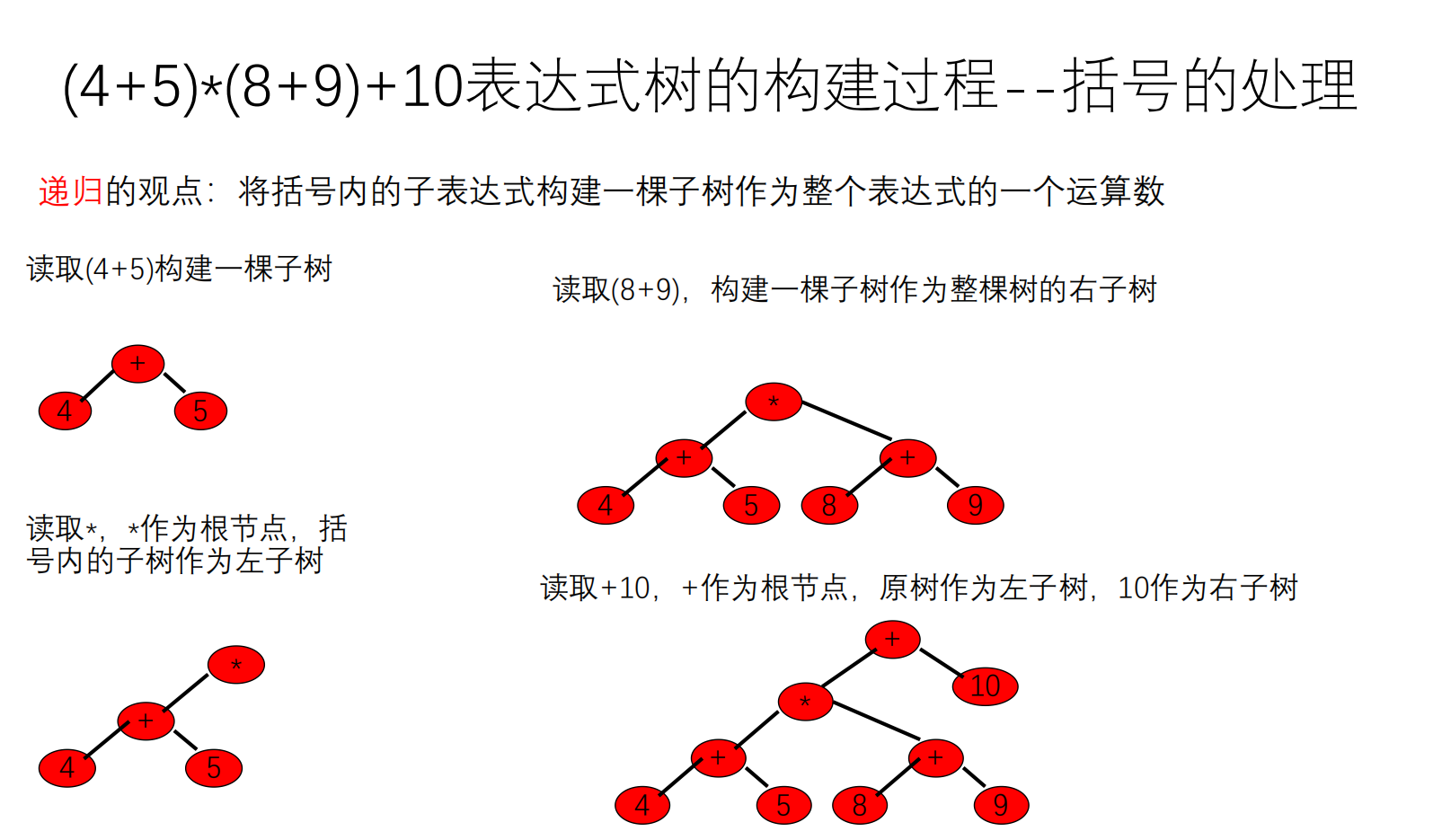
表达式树

简单版：

先考虑加减乘除
先获取第一个运算数和第一个运算符，第一个运算数作为第一个运算符的左孩子
继续顺序扫描中缀表达式，直到结束
	运算数：将此运算数作为前一运算符的右孩子。
	新运算符优先级小于等于根运算符，则新运算符作为根，原来的树作为该根的左子树
	新运算符优先级高于根运算符，新运算符作为原根节点的右儿子，原来的右子树作为当前运算符的左子树，继续构建右子树。
	注：左右子树先计算完再计算根所代表的计算

稍作修改：

顺序扫描中缀表达式，直到结束
	运算数：如果已存在运算树，将此运算数作为前一运算符的右孩子（如果当前右子树为空，此运算数成为根的右儿子，如果右子树非空，则为右子树的右儿子），否则存储该运算数
	运算符
		+-：如果不存在运算树，此运算符作为根，存储的运算数作为左儿子。否则新运算符作为根，原来的树作为该根的左子树
		*/：如果不存在运算树，此运算符作为根，存储的运算数作为左儿子。否则
			根运算符为*/，则新运算符作为根，原来的树作为该根的左子树（此时新运算树的右子树为空）
			根运算符为+-，新运算符作为原根节点的右儿子，原来的右子树作为当前运算符的左子树，继续构建右子树。 （此时新运算树的右子树的右儿子为空）

哈夫曼树

在计算机中每个字符是用一个编码表示。哈夫曼树是一棵最小代价的二叉树，在这棵树上，所有的字符都包含在叶节点上。

要使得整棵树的代价最小，显然权值大的叶子应当尽量靠近树根，权值小的叶子可以适当离树根远一些。

哈夫曼算法

给定一个具有n个权值 $\{ w_1 ,w_2 ,………w_n \}$ 的节点的集合，构造集合 $F= \{ T_1 ,T_2 ,………T_n \}$ ，其中每个 $T_i$ 为只有根节点的二叉树， $T_i$ 的权值为 $w_i$
执行 i = 1 至 n -1 的循环，在每次循环时执行以下操作

a) 从当前集合中选取权值最小、次最小的两棵树，以这两棵树作为新树 $b_i$ 的左右子树， $b_i$ 的权值为其左右子树权值之和。

b) 在集合中去除这两个权值最小、次最小的树，并将新树 $b_i$ 加入其中。这样，在集合 $F$ 中，树的数量便减少了一个。

c) 这样，在经过了 $n-1$ 次循环之后，集合F中只剩下了一棵树，即为所求哈夫曼树

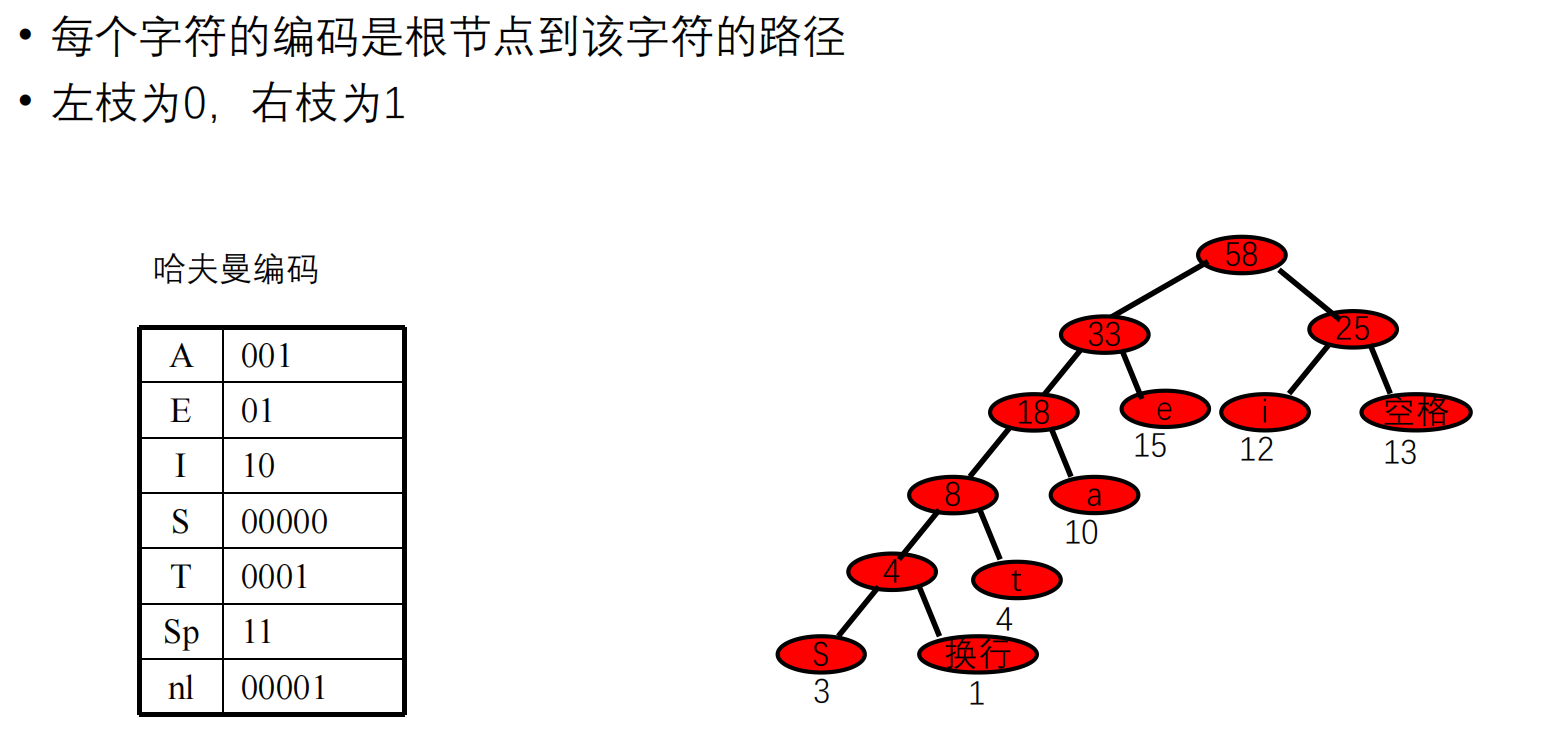
哈夫曼编码

哈夫曼树

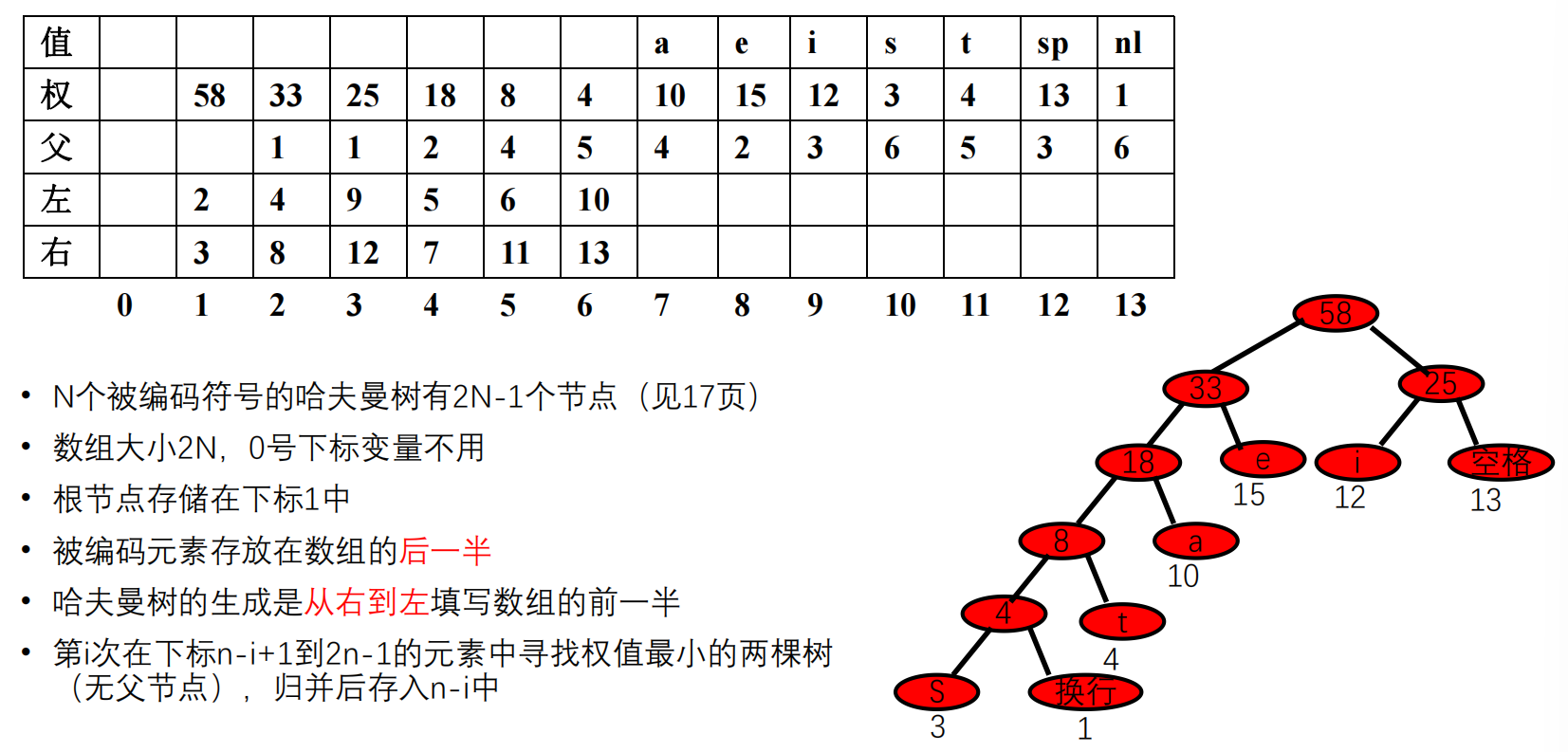
存储：用数组存三叉链表

哈夫曼树类实现：

具体实现代码

template 
    class hfTree{
        private:
        struct Node { //保存Huffman树的数组中的元素类型
            Type data; //节点值
            int weight; //节点的权值
            int parent, left, right;
        };
        Node *elem;
        int length;
        public:
        struct hfCode { //保存编码的类型
            Type data; //字符
            string code; //编码
        };
        hfTree(const Type *x, const int *w, int size);
        void getCode(hfCode result[ ]); //由Huffman树生成编码
        ~hfTree() { delete [ ] elem; }
    };
template 
    hfTree::hfTree(const Type *v, const int *w, int size)
        //待编码的符号，符号的权值，符号的数量
    {
        const int MAX_INT = 32767;
        int min1, min2; //最小树、次最小树的权值
        int x, y; //最小树、次最小树的下标
        //置初值
        length = 2 * size;
        elem = new Node[length];
        for (int i = size; i < length; ++i) {
            elem[i].weight = w[i - size];
            elem[i].data = v[i - size];
            elem[i].parent = elem[i].left = elem[i].right = 0;
            //都是只有根节点的树
        }
        // 构造新的二叉树
        for (i = size - 1; i > 0; --i) {
            min1 = min2 = MAX_INT; x = y = 0;
            for (int j = i + 1; j < length; ++j)
                if (elem[j].parent == 0)
                    if (elem[j].weight < min1) {
                        min2 = min1; min1 = elem[j].weight;
                        x = y; y = j;
                    }
            else if (elem[j].weight < min2) {
                min2 = elem[j].weight;
                x = j;
            }
            elem[i].weight = min1 + min2;
            elem[i].left = x; elem[i].right = y;
            elem[i].parent = 0; elem[x].parent = i;
            elem[y].parent = i;
        }
    }
template 
    void hfTree::getCode(hfCode result[]){
        int size = length / 2, p, s;
        for (int i = size; i < length; ++i) {
            result[i - size].data = elem[i].data;
            result[i - size].code = “”; //编码初始为空
            p = elem[i].parent;
            s = i;
            while (p) { //直到根节点
                if (elem[p].left == s)
                    result[i - size].code = '0' + result[i - size].code;
                else result[i - size].code = '1' + result[i - size].code;
                s = p;
                p = elem[p].parent;
            }
        }
    }
int main()
{
    char ch[] = {"aeistdn"};
    int w[] = {10,15,12,3,4,13,1};
    hfTree tree(ch, w, 7);
    hfTree::hfCode result[7];
    tree.getCode(result);
    for (int i=0; i< 7; ++i)
        cout << result[i].data << ' ‘ << result[i].code << endl;
        return 0;
}

树和森林

链式前向星（孩子链表示法）

struct edge {
    int next;
    int to;
    int w;    // 若果有的话
} e[N];
int cnt = 0;
void add_edge(int u, int v, int w) {
    cnt ++;
    e[cnt].to = v;
    e[cnt].w = w;           // 若果有的话
    e[cnt].next = head[u];
    head[u] = cnt;
}
//便历邻边
for (int i = head[u]; i != 0; i = e[i].next) {
    ...
}

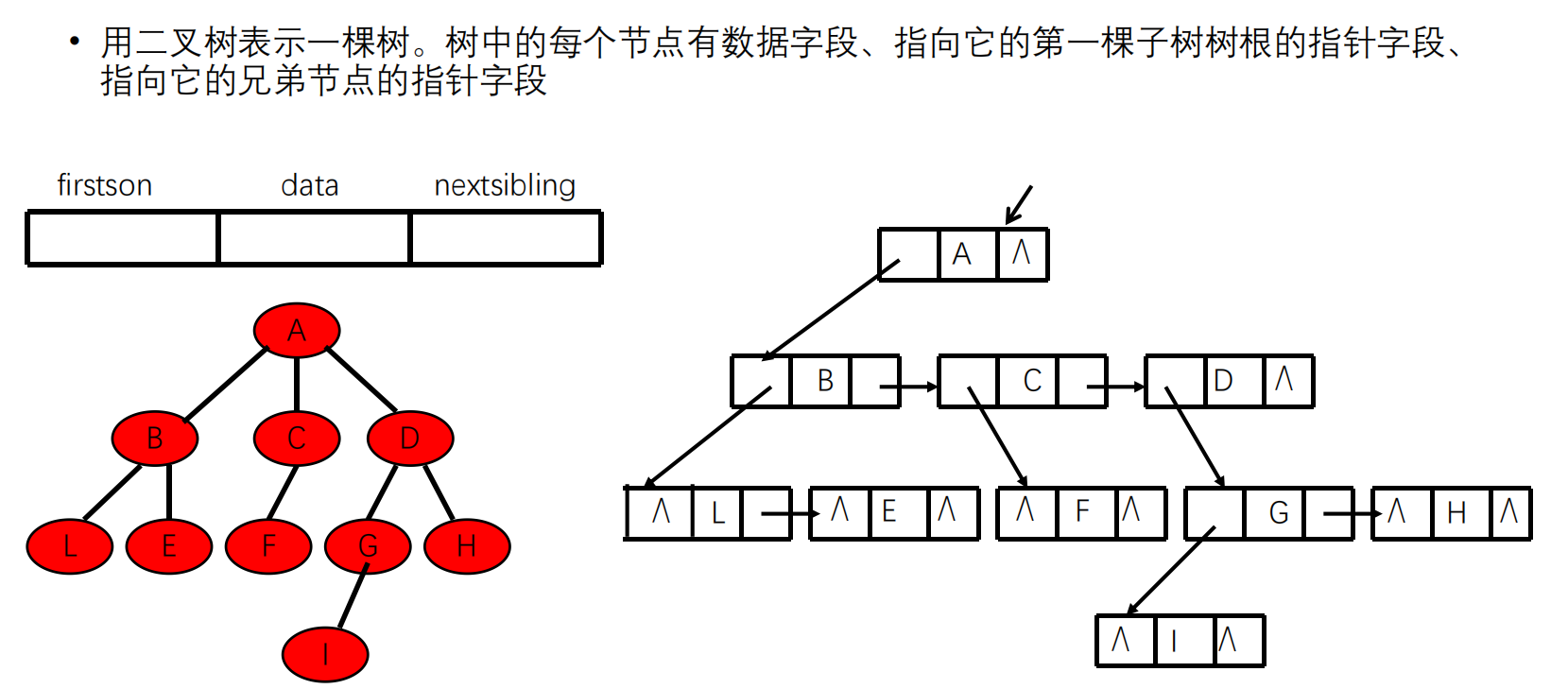
孩子兄弟链表示法

双亲表示法

只存父亲节点

森林的二叉树表示

将每棵树Ti转换成对应的二叉树 $B_i$ （把树换成孩子兄弟链即可）

将 $B_i$ 作为 $B_{i-1}$ 根节点的的右子树

20 优先级队列

优先级队列：节点之间的关系是由节点的优先级决定的，而不是由入队的先后次序决定。优先级高的先出队，优先级低的后出队。

二叉堆

在算法笔记中详细介绍过，这里简单地粘贴过来：

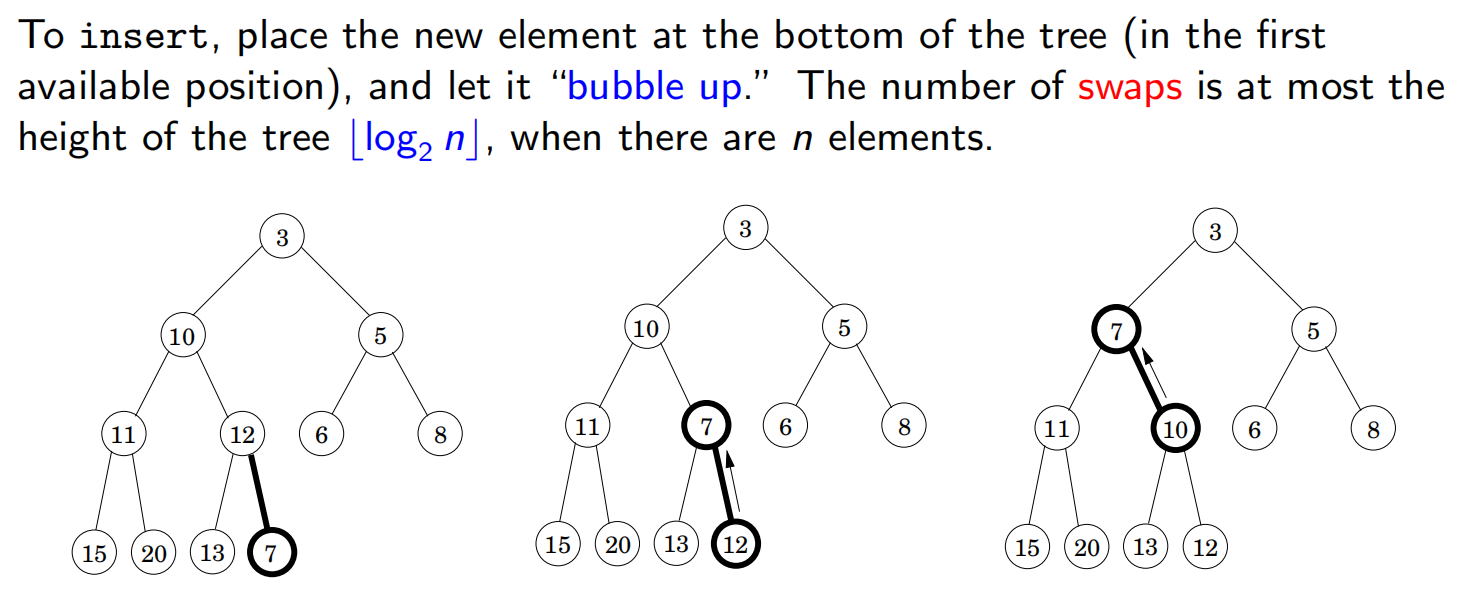
元素被存储在一个完全二叉树中，即二叉树每层上的节点都被从左到右地填满，并且在上一层未填满之前不会出现下一层。另外，需要遵循一种特殊的顺序：树中任意节点的键值必须小于等于其后裔节点的键值。因此，特别的，根节点一定对应着键值最小的元素。

插入（Insert）：先插入到尾部，然后不断和父亲交换（称为冒泡） $O(log\ n)$

减少键值（decreakey）和插入类似。

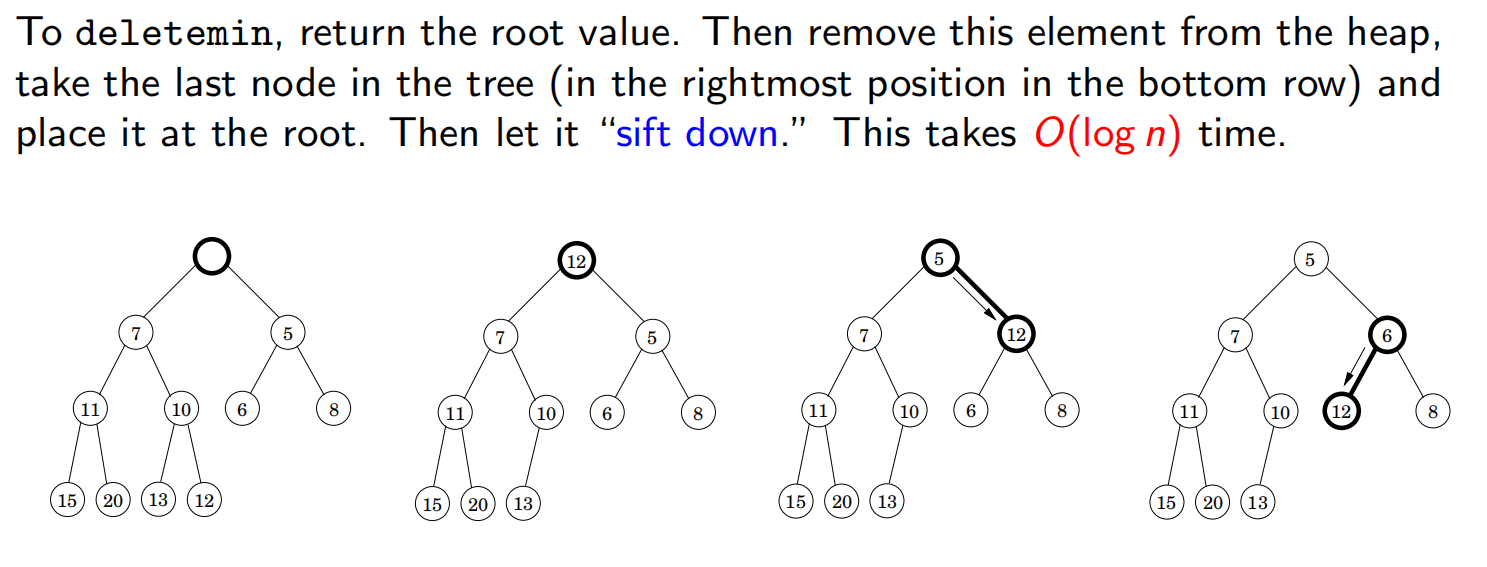
删除最小元素（deletemin）：删除根，用尾部元素代替这个根，然后再不断地和所有孩子比较并交换。时间复杂度： $O(log\ n)$

void up(int x) {
  while (x > 1 && h[x] > h[x / 2]) {
    std::swap(h[x], h[x / 2]);
    x /= 2;
  }
}

void down(int x) {
  while (x * 2 <= n) {
    t = x * 2;
    if (t + 1 <= n && h[t + 1] > h[t]) t++;
    if (h[t] <= h[x]) break;
    std::swap(h[x], h[t]);
    x = t;
  }
}

建堆：具体可以看Slides（20 优先级队列）中的动画或者 oiwiki

首先先直接把所有数挨个放进去构成一个完全二叉树，然后两种方法：

从根开始，for (i = 1; i <= n; i++) up(i); $O(nlogn)$
从叶子开始，for (i = n; i >= 1; i--) down(i); $O(n)$

如何使初始建堆后每一步堆操作都是 $O(logN)$ ?doublespace是 $O(N)$ $\Rightarrow$ 链表,而且是三叉链表

排队系统的模拟

其他堆

左堆、斜堆、二项堆支持堆的归并

D堆

d个儿子

左堆

满足堆的有序性，但平衡稍弱一些的堆，不要求是完全二叉树

空路径长度(npl)：为x到不满两个孩子的节点的最短路径，即具有0个或一个孩子的节点的npl为0，npl(nullptr) = -1

左堆：对每个节点x，左孩子的npl不小于右孩子的npl

节点的NPL = min(它的右孩子的NPL ,它的左孩子的NPL)+1=它的右孩子的NPL + 1

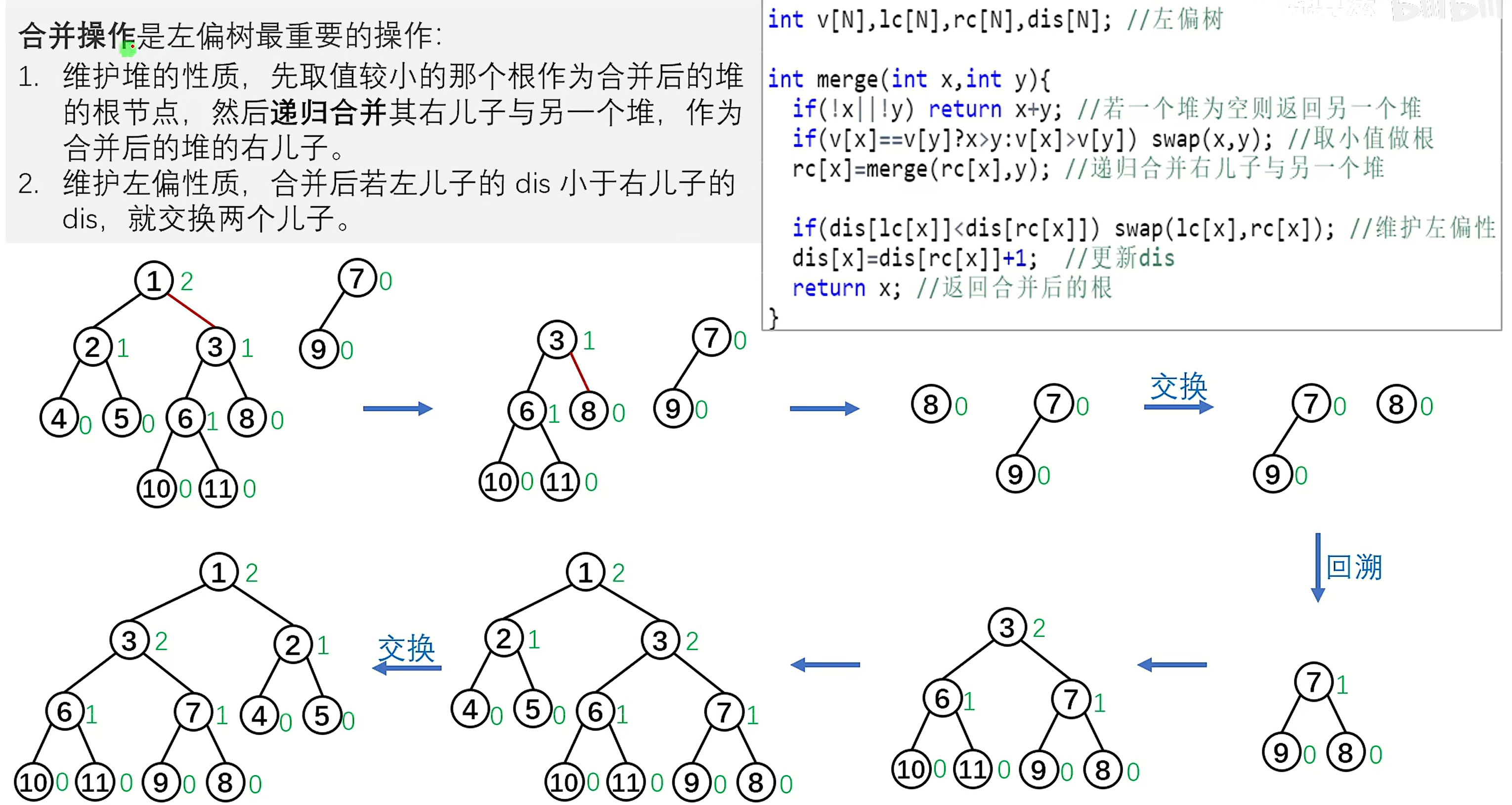
合并操作：

int merge(int x, int y) {
    if (!x || !y) 
        return x | y;  // 若一个堆为空则返回另一个堆
    if (t[x].val > t[y].val) 
        swap(x, y);  // 取值较小的作为根
    t[x].rs = merge(t[x].rs, y); // 递归合并右儿子与另一个堆
    if (t[t[x].rs].d > t[t[x].ls].d)
        swap(t[x].ls, t[x].rs);   // 若不满足左偏性质则交换左右儿子
    t[x].d = t[t[x].rs].d + 1;  // 更新NPL
    return x;
}

入队：将入队元素看成是只有一个元素的左堆，归并两个左堆就形成了最终的结果

出队：删除了根节点后，这个堆就分裂成两个堆。重新归并两个堆

斜堆

斜堆是左偏树的自适应形式。当合并两个堆时，它无条件交换合并路径上的所有节点，以此试图维护平衡。

均摊的 $O(logN)$ 的时间复杂度。

即，左堆中的 if (t[t[x].rs].d > t[t[x].ls].d) swap(t[x].ls, t[x].rs); 改为无条件 swap(t[x].ls, t[x].rs);

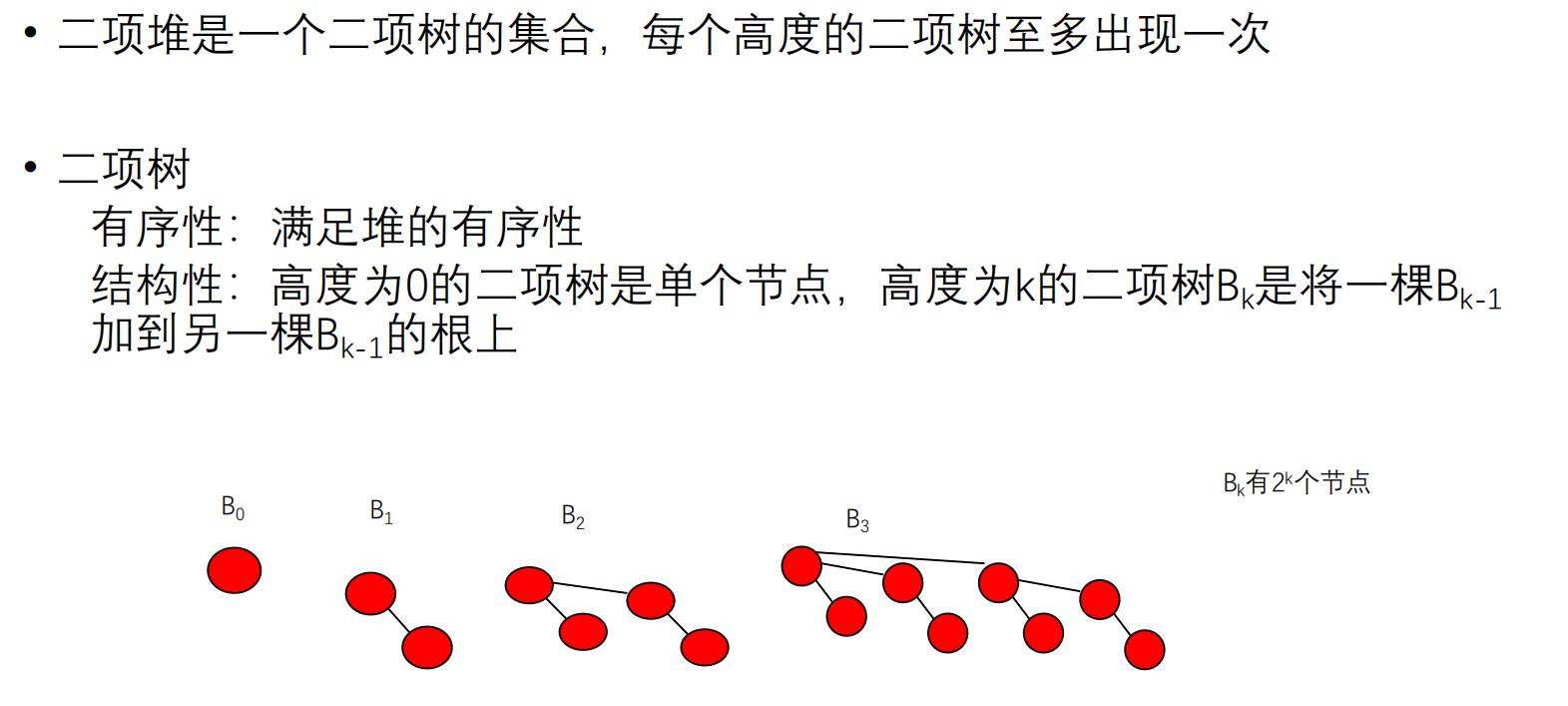
二项堆

二项堆是一个二项树的集合，每个高度的二项树至多出现一次

优先级队列的表示

用一个二项堆存储

因为 $B_k$ 有 $2k$ 个节点，所以堆的结构是唯一的，正好对应元素数的二进制表示

如13可表示为1101，则13个元素的优先级队列由 $B_3$ 、 $B_2$ 和 $B_0$ 组成

这一篇博客写的蛮清楚的，建议看这个。

杨氏矩阵

插入的时候先插入到 (m,n) ，然后上浮。删除最小元素把它设置为无穷，然后下沉。

具体实现

STL中的优先级队列

priority_queue：默认最大堆，

heap：作为priority_queue的底层实现

主要成员：

void push( const Object &x)
const Object &top() const
void pop()
bool empty()
void clear()
没有迭代器，无遍历功能

21 集合与静态查找表

在集合中，每个数据元素有一个区别于其它元素的唯一标识，通常称为键值或关键字值（Key）

静态查找表：元素个数不变，元素值不变，通常用顺序表存储（vector,seqList,数组）

无序表查找

template <class KEY, class OTHER>
    int seqSearch(SET<KEY, OTHER> data[ ], int size, const KEY &x){
    data[0].key = x;
    for (int i = size ; x != data[i].key; --i);
    return i;
}

利用第0个元素作为哨兵减少n次比较（不用在每次循环体中检查i < currentLength && data[i] != x ）

有序表查找

利用关键字的次序优化查找过程

顺序查找

二分查找

int low = 1, high = size, mid;
while (low <= high ) {
    mid = low + (high - low) / 2;
    if ( x == data[mid].key ) return mid;
    if ( x < data[mid].key) high = mid - 1;
    else low = mid + 1;
}
return 0;

插值查找

适用于数据分布比较均匀的情况。比较次数小，计算量大。比如，数据存储在磁盘而非内存里的时候就可以使用。

1	next=low+(x-a[low])/(a[high]-a[low])*(high-low+1)

分块查找

STL中的静态查找表

find：顺序查找

template <class InputIterator, class T>
    InputIterator find(InputIterator first, InputIterator last, const T& value){
    //查找范围[first,last)
    while(first != last && *first != value) ++first;
    return first;
}

binary_search：二分查找

template <class ForwardIterator, class T, class Compare>
    //使用函数对象comp，即operator()比较
    bool binary_search(ForwardIterator first, ForwardIterator last, const T& value, Compare comp){//默认小于
    ForwardIterator i=lower_bound(first, last, value, comp);
    return i!=last && !comp(value, *i);
}

lower_bound：指向第一个大于等于val的位置

upper_bound：指向第一个大于val的位置

22 动态查找表

目标：既要支持快速查找，又要方便插入删除

方案：

树：借鉴二叉堆的思想，让操作与树高有关， $O(logN)$ 的时间复杂度

哈希表

二叉查找树

oiwiki-二叉搜索树、平衡树

空树是二叉搜索树。
若二叉搜索树的左子树不为空，则其左子树上所有点的附加权值均小于其根节点的值。
若二叉搜索树的右子树不为空，则其右子树上所有点的附加权值均大于其根节点的值。
二叉搜索树的左右子树均为二叉搜索树。

排序：中序遍历

插入：

//公有插入函数
template <class KEY, class OTHER>
    void BinarySearchTree<KEY, OTHER>::insert( const SET<KEY, OTHER> & x ){
        insert( x, root );
    }
//私有插入函数
template <class KEY, class OTHER>
    void BinarySearchTree<KEY, OTHER>::insert( const SET<KEY, OTHER> & x, BinaryNode *&t ){//为什么要引用？使得新增节点与其父节点关,即父节点的某个孩子指针会发生变化
        if( t == nullptr ) 
            t = new BinaryNode( x, nullptr, nullptr );
        else if( x.key < t->data.key ) 
            insert( x, t->left );
        else if( t->data.key < x.key ) 
            insert( x, t->right );
    }

删除节点将会使树分裂成几个部分

删除叶节点：直接删除，更改它的父亲节点的相应指针字段为空

删除有一个儿子的节点：子承父业

删除有两个儿子的节点：选取“替身”，删除替身：左子树的最大值或右子树的最小值

如何使被删节点的儿子和父亲连接起来？用引用传递

template <class KEY, class OTHER>
    void BinarySearchTree<KEY, OTHER>::remove( const KEY & x, BinaryNode * & t ){
        if( t == nullptr ) return;
        if ( x < t->data.key ) remove( x, t->left );
        else if( t->data.key < x ) remove( x, t->right );
        else if( t->left != nullptr && t->right != nullptr ) { //有两个孩子
            BinaryNode *tmp = t->right;
            while (tmp->left != nullptr) tmp = tmp->left; //找右子树最小的
            t->data = tmp->data;
            remove( t->data.key, t->right );//为什么不是remove(t->data.key,tmp)?
        }
        else { //被删节点是叶节点或只有一个孩子
            BinaryNode *oldNode = t;
            t = ( t->left != nullptr ) ? t->left : t->right;
            delete oldNode;
        }
    }

平衡二叉查找树

（首先满足二叉查找树的性质）常用的平衡树：AVL树，红黑树，AA树

AVL树

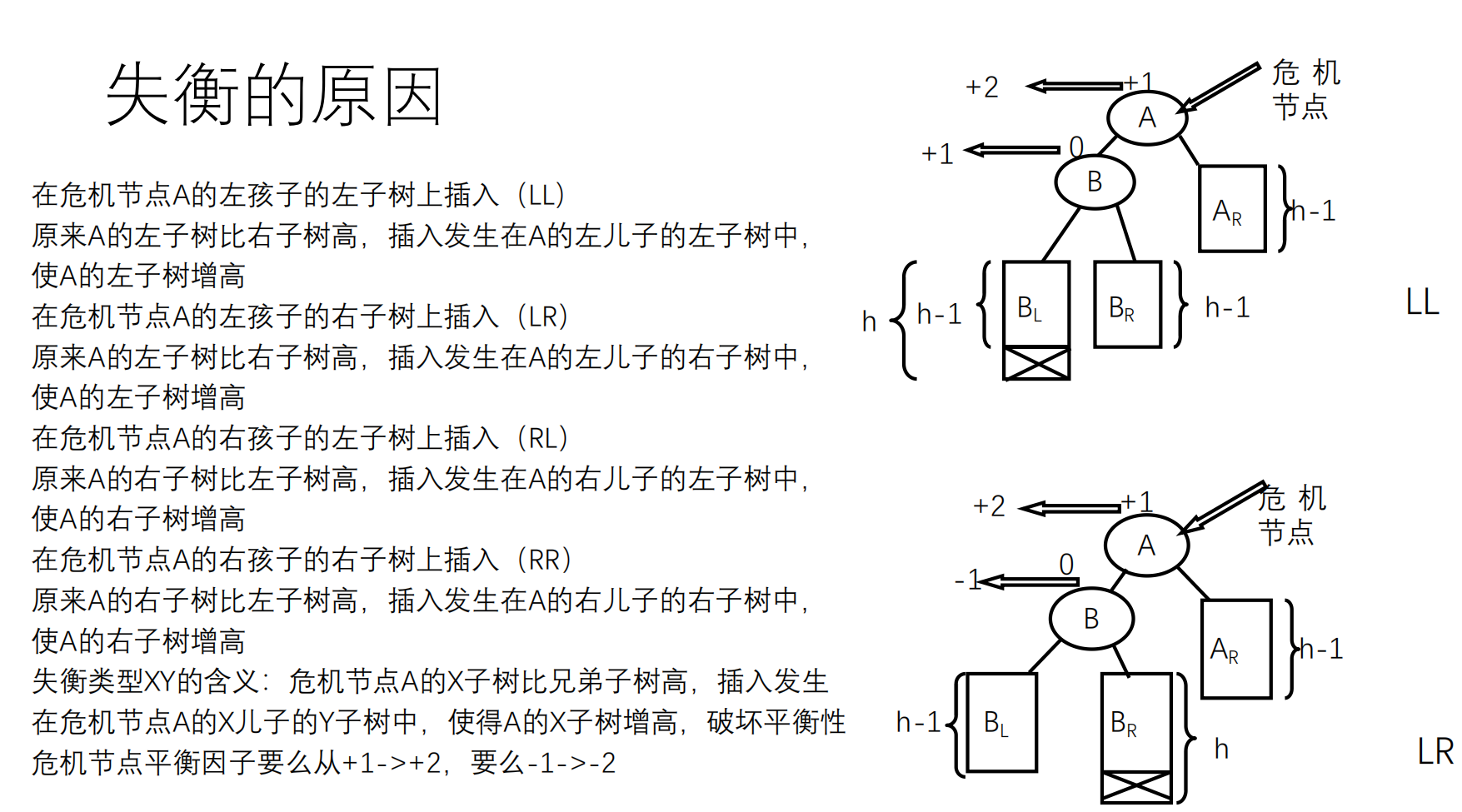
平衡因子（平衡度）：节点的平衡度是节点的左、右子树的高度差

AVL树：每个节点的平衡因子都为 +1、-1、0 的二叉树。

每一个node额外保存一个高度信息，平衡信息通过子树高度计算。

插入：

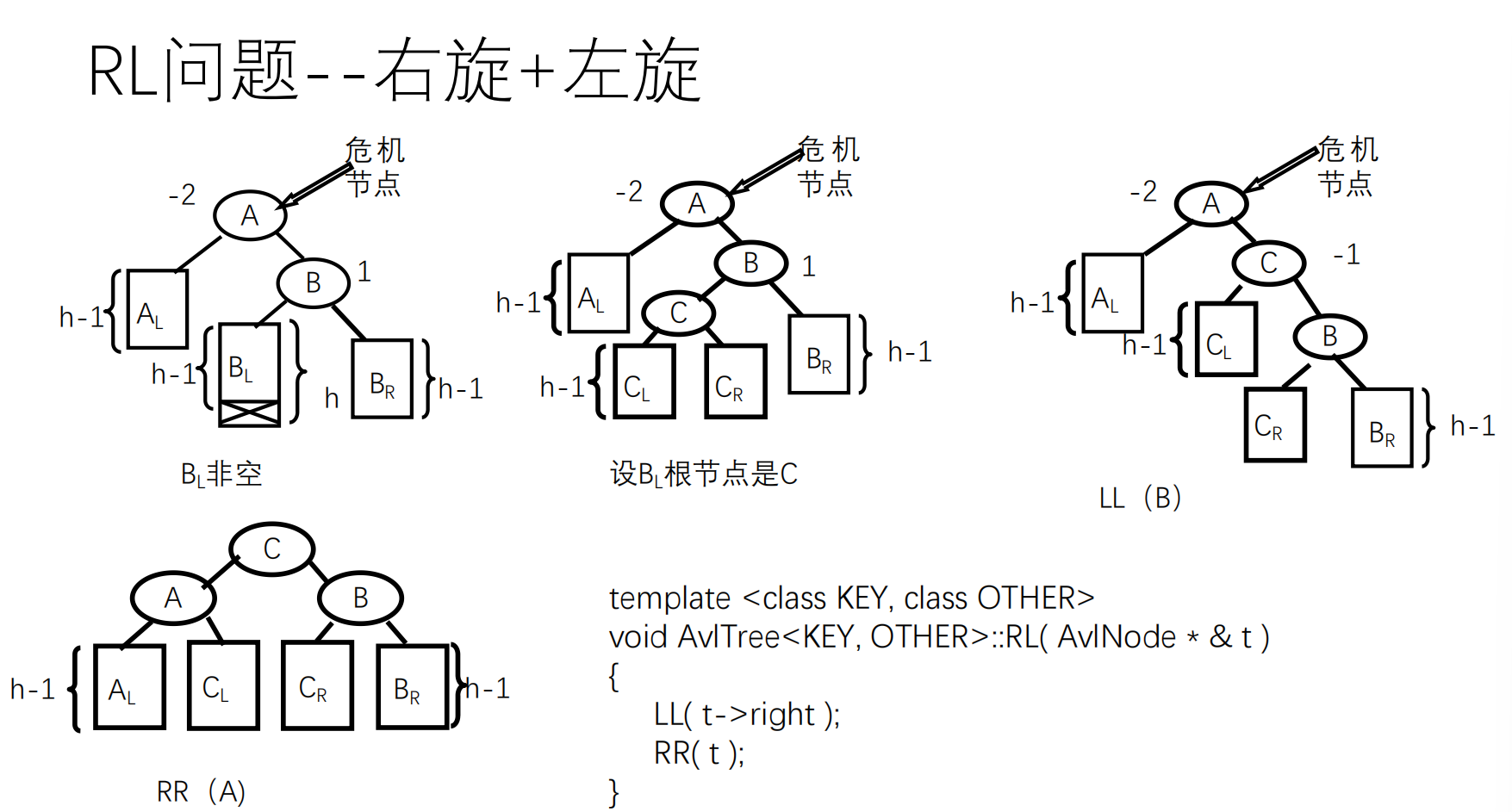
先按照二叉查找树的方式插入，然后调整平衡（用到四个函数：LL,LR,RL,RR）

调整平衡：自插入节点开始，向根节点回溯

如果没有破坏平衡，只需修改平衡因子
如果失去平衡，通过旋转恢复平衡

平衡的调整过程参阅 oiwiki .

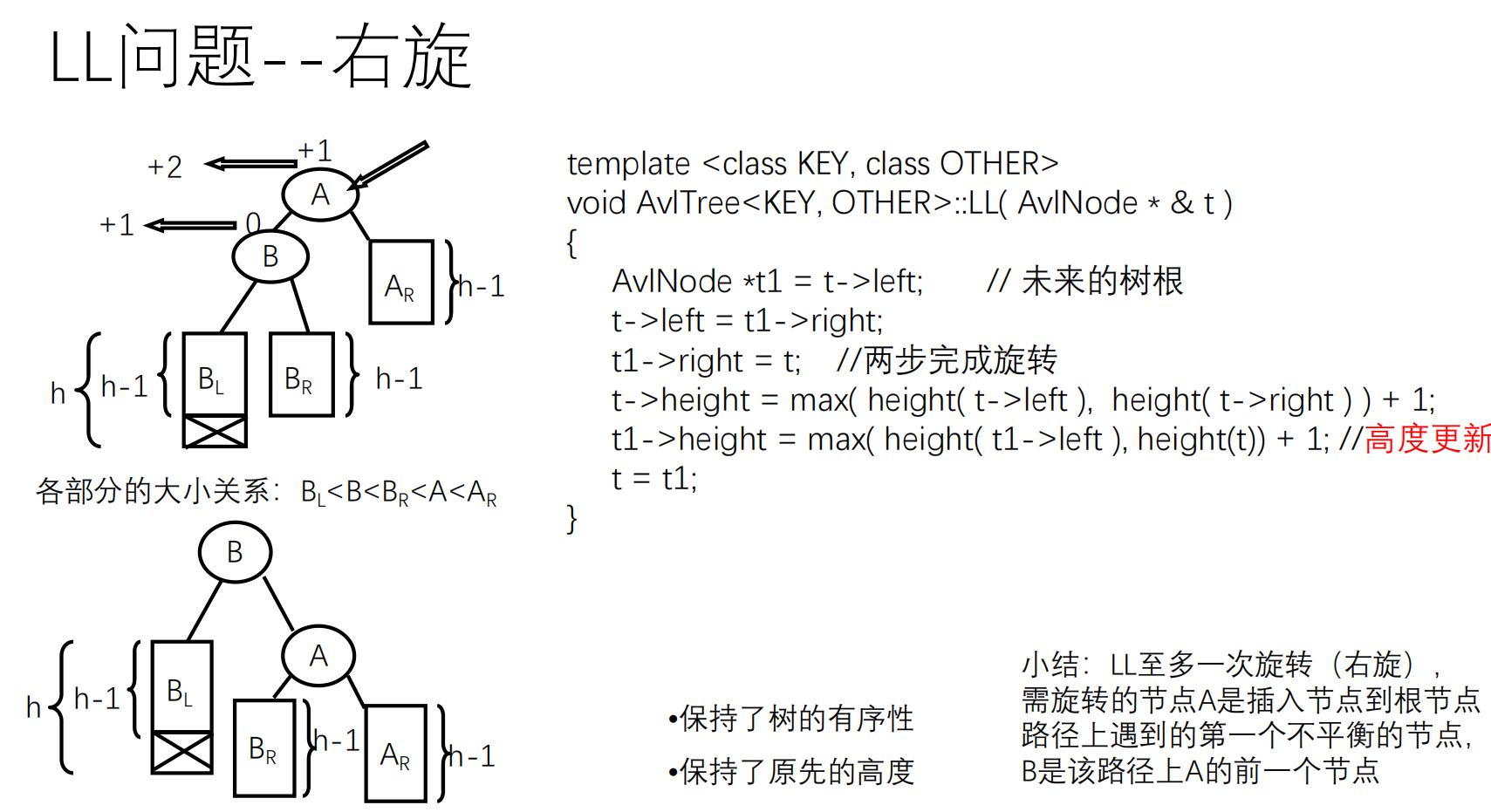
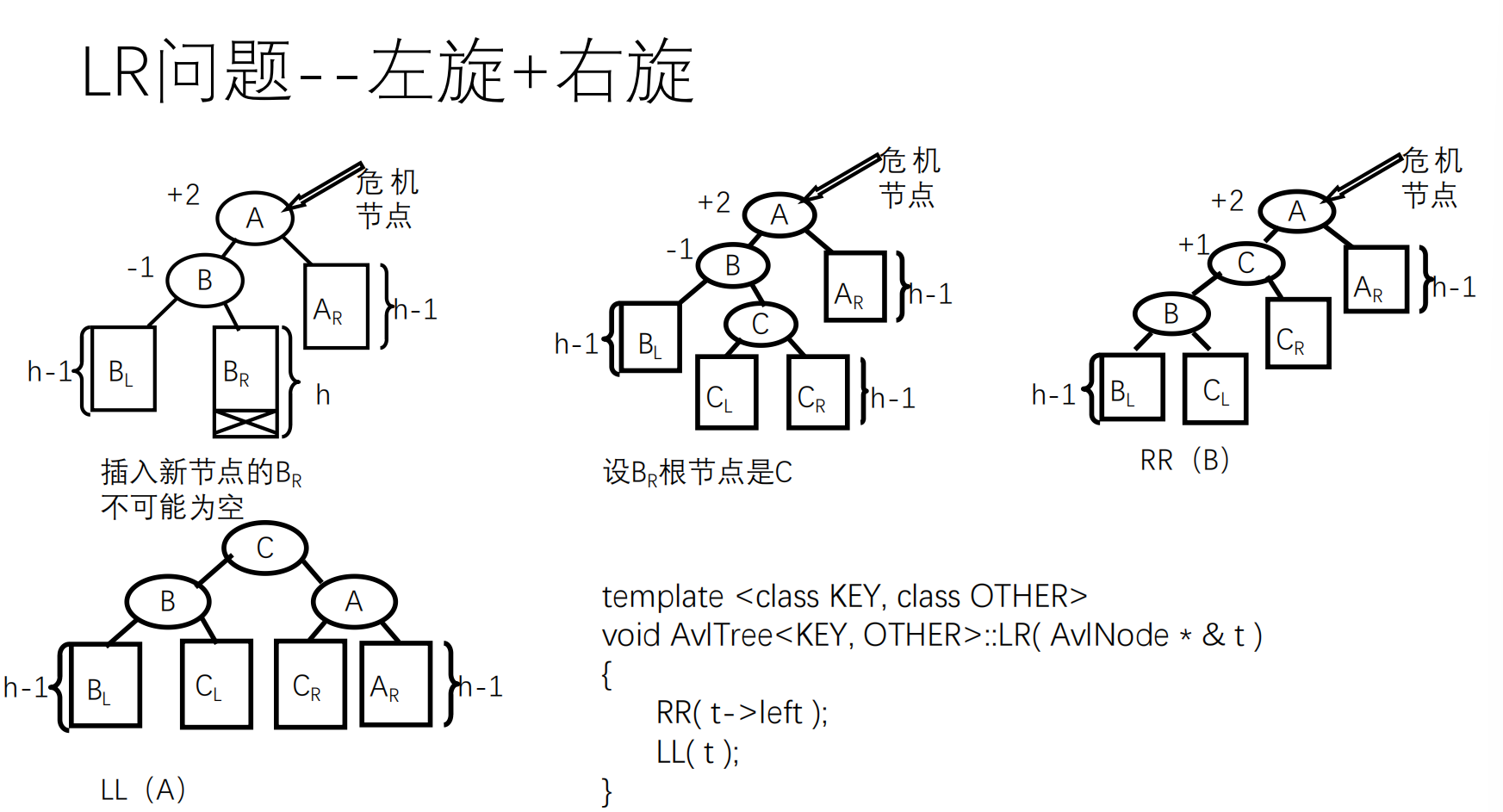
TreeNode* rotateLeft(TreeNode* root) {
    TreeNode* newRoot = root->right;
    root->right = newRoot->left;
    newRoot->left = root;
    // 更新相关节点的信息
    updateHeight(root);
    updateHeight(newRoot);
    return newRoot;  // 返回新的根节点
}

TreeNode* rotateRight(TreeNode* root) {
    TreeNode* newRoot = root->left;
    root->left = newRoot->right;
    newRoot->right = root;
    updateHeight(root);
    updateHeight(newRoot);
    return newRoot;
}

oiwiki截图

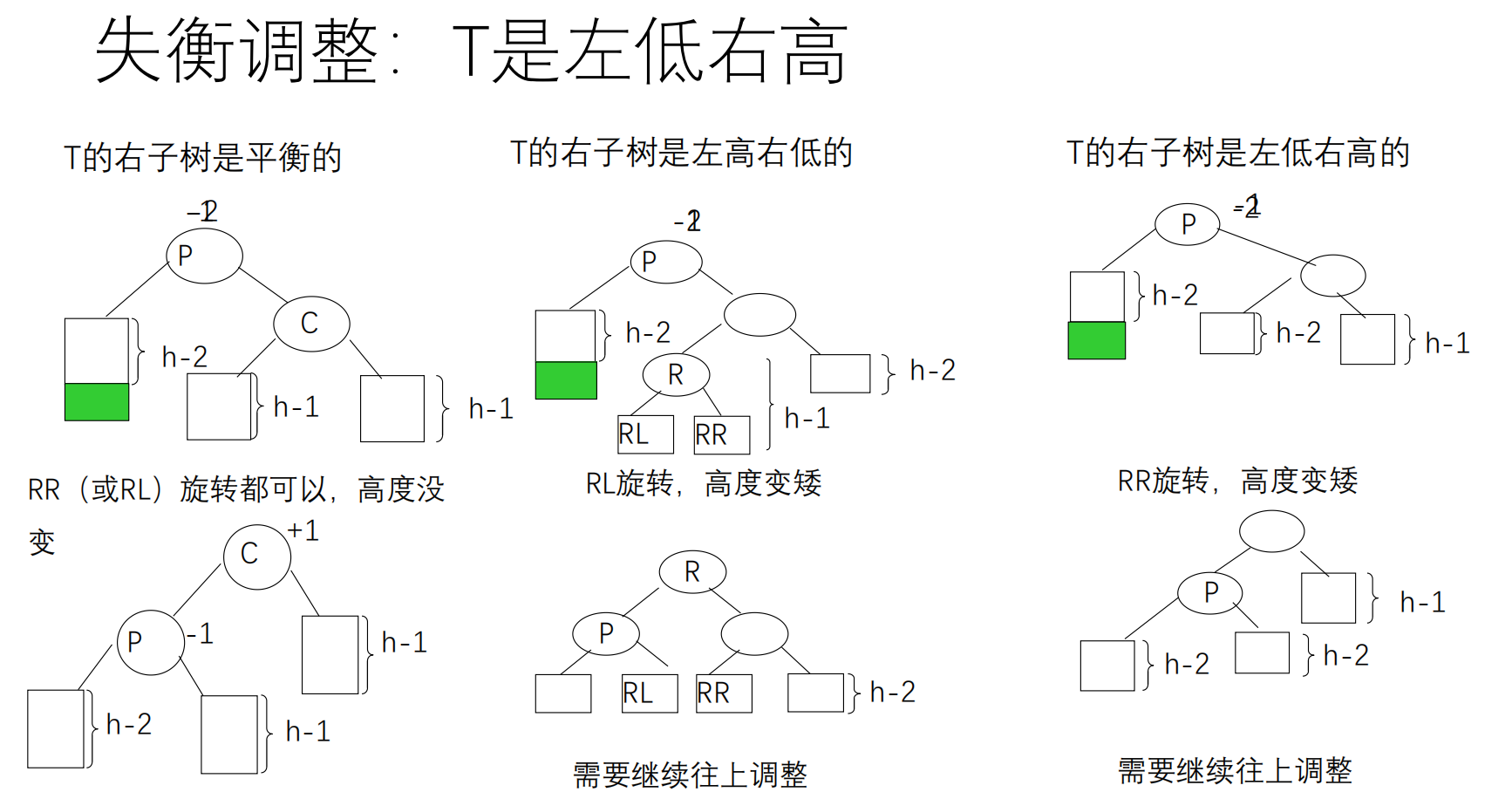
删除：

在删除了一个节点后，沿着到根节点的路径向上回溯，随时调整路径上的节点的平衡度。

删除时，子树可能变矮。只有当某个节点的高度在删除前后保持不变，才无需继续调整。

递归的删除函数有一个布尔型的返回值。当返回值为true时，调整停止。当返回值为false时，继续调整。

假设都在T的左子树删除，使左子树高度变矮：

删除前：

可视化网站

具体代码见Slides。

伸展树（Splay树）

基本思想：让10%经常访问的数据靠近根节点

基本方法：在每个节点被访问后，通过一些旋转使它向根移动

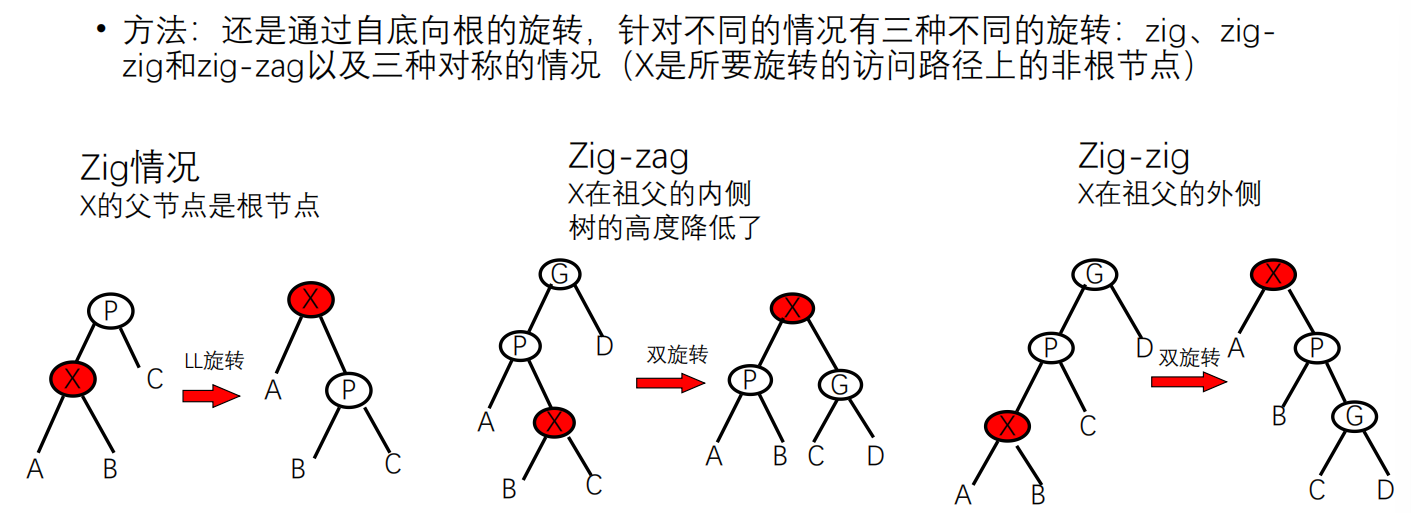
要求：不仅向根旋转，还要降低树的高度，从而能在自底向上的伸展过程中使树更加平衡，能得到对数的均摊上界

oiwiki截图说实话没看懂…啥时候问问大佬

22-2 红黑树

一个做的非常好的动画：

红黑树-定义，插入，构建

红黑树-删除

实现参考大作业实现：Project4-ESet

22-3 文本压缩

将文本字符串映射为数字编码

首先该文本串中所有可能出现的字母分配一个代码

例：压缩文本串S=aaabbbbbbaabaaba，则a的代码为0，b的代码为1

其次构造字符串和编码的映射关系并存储在一个代码表中，表中元素为数对(key, value)，其中key是字符串，value是字符串的代码。

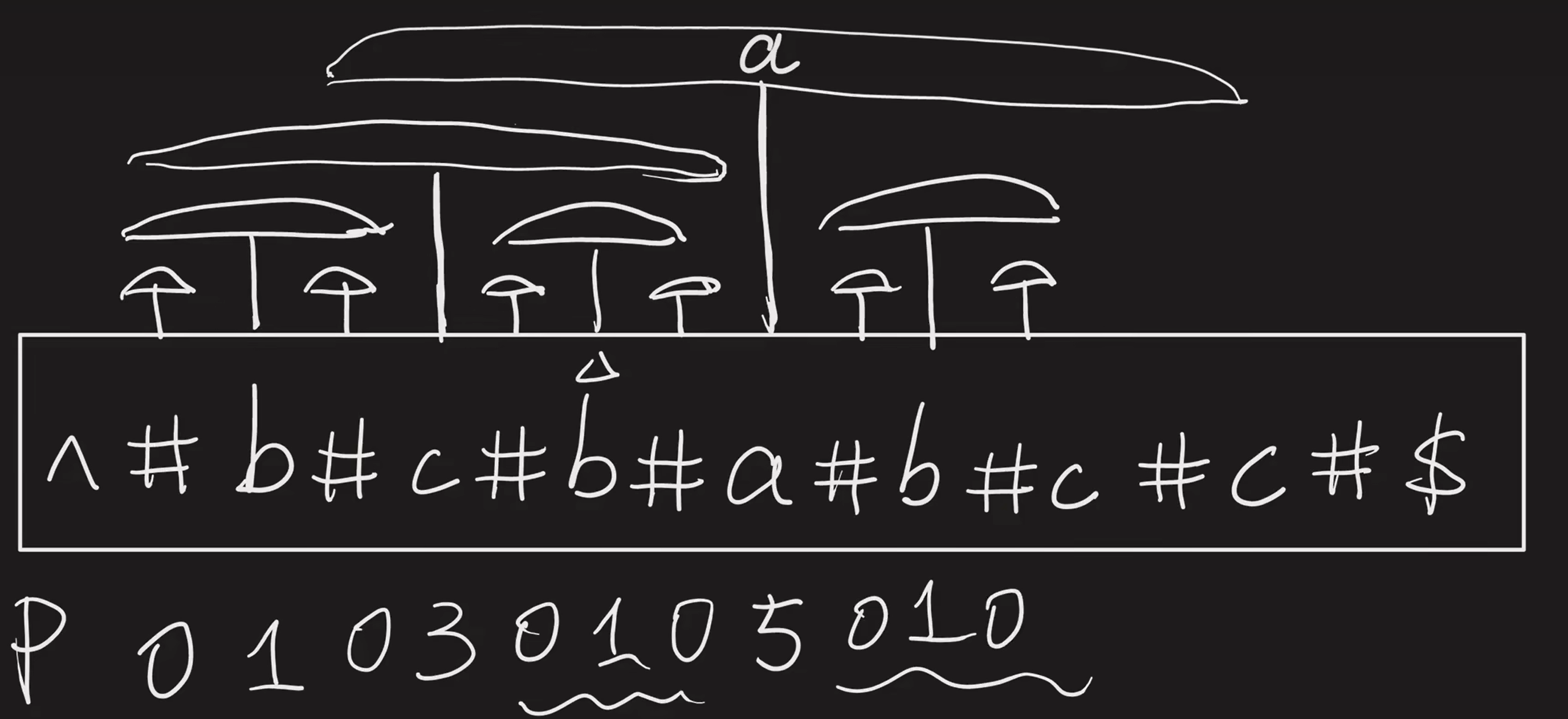
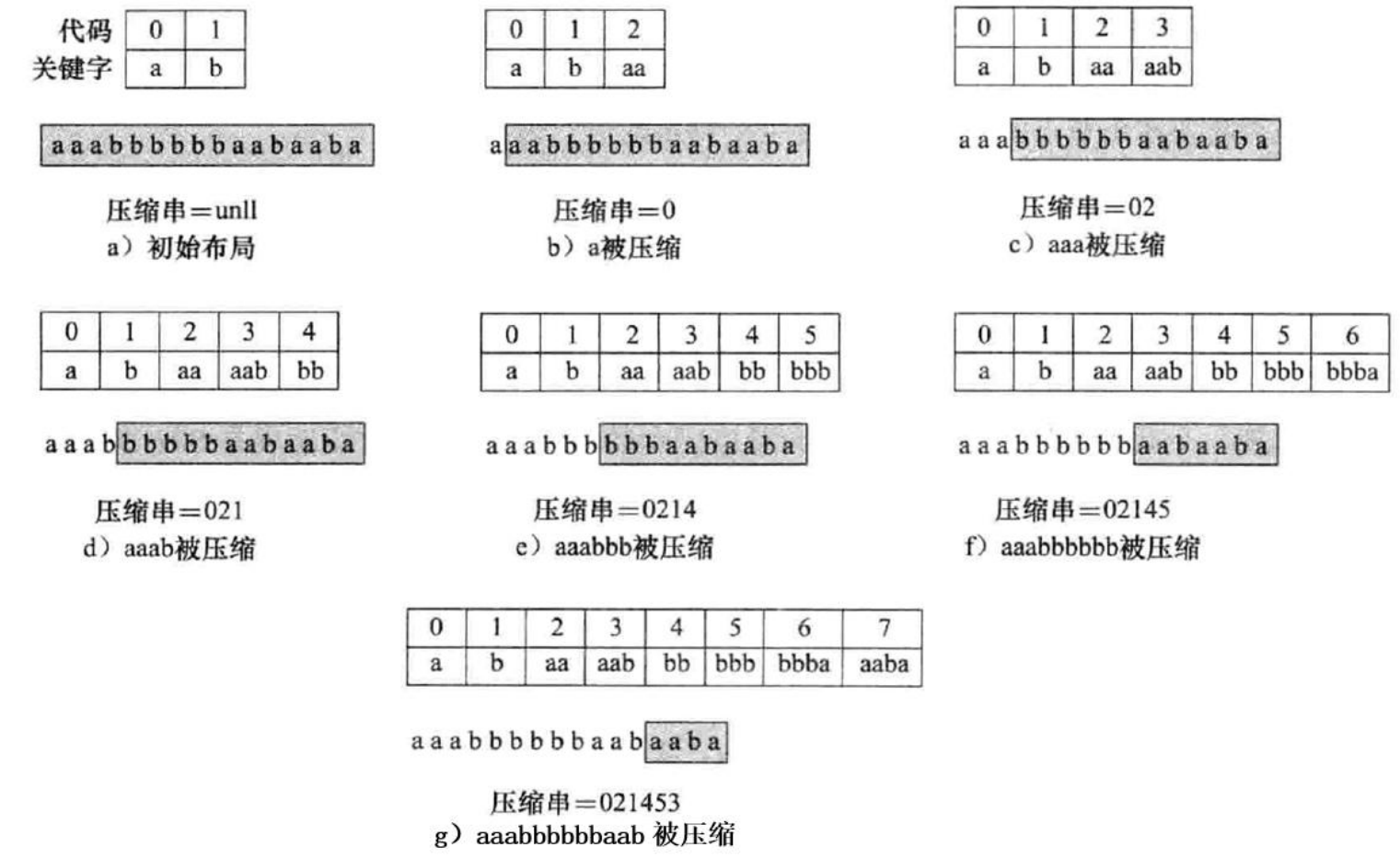
LZW规则

从初始表开始，不断在文本串S的未编码部分中寻找于表中一个字符串相匹配的最长的字符串，并输出其代码。这个字符串称为前缀，用p表示。

p是最长的字符串，是指如果在S中存在下一个字符c，则需要为pc分配一个新的代码并将其放入代码表

如下图：每一幅图中，在未编码的（灰色字符串）中找最长的在字典中的作为前缀，如b图中的是aa，加一个字符（向后延一个）b得到aab，加入字典中（得到图c中的字典）

代码表：利用动态查找表存储，不是压缩文件的组成部分。

LZW解压缩

每次输入一个代码，然后把代码替换为相应文本，从代码到文本的映射（代码表）将重新构造

把分配给单一字符的代码放入代码表，但此时是根据给定的代码去查找记录（而不是根据文本），因此现在的(key, value)中key是代码，value是对应的文本。

压缩文件中第一个代码对应于一个单一字母，可以直接替换为该字符

对于压缩文件中其它代码p，两种情况（图中右侧）：

23 外部查找与排序

外存储器

主存储器也被称为内存，是存储正在运行的程序代码及处理数据。内存存取速度快，容量小，价格贵。

外存储器用于存储长期保存的信息。常用的外存储器有磁盘、磁带、光盘、U盘等。具有存储量大、价格低廉和永久保存等优点，但也有访问速度慢、不能被程序直接访问等缺点。

磁带：顺序存取的设备。磁带的使用，从根本上就绕开了随机访问、随机读写相关的问题，磁带的使用是高度有序的、连续的、少次大量的，数据在磁带上是一个系列一个系列地成组排列磁带存储主要的挑战就是读写速度慢，但是在归档、备份这种对延迟要求不是很高的领域，就有着很大的优势

一些其他知识，不知道考不考

外部查找

内部查找：一个节点存放一条数据，每次访问一个节点

外部查找：每次访问一个数据块（页），一个数据块内可以存放多条数据（外存中的数据元素通常称为记录）

B树

同样的，贴上做的非常好的动画：

B树(B-树)- 来由, 定义, 插入, 构建

B树(B-树) - 删除

实现见oiwiki

B+树

动画视频（但是这个只是基本定义）：

B+树基本操作

知乎讲解

实现参考大作业实现：Project5-BPlusTree

M：在 B 树中代表树的阶数。
L：表示 B 树叶子节点中最多能存储的数据记录数量。

一个块存放一个节点能使IO效率最高。假设一个块的容量8,192字节

M的选择：如果每个键要占用32字节。因此在一棵M阶B树中，可以有M-1个键，总的数据量就是32M-32个字节加上M个分支。而且因为每个分支其实是另一个磁盘块的块号，假设分支的大小是4个字节。那么分支就要占去4M个字节。则一个非叶子节点总的内存需要量是36M-32字节。要36M-32不超过8,192的M的最大值是228，于是选择 M=228。

B+树的时间效益：

查找至多需要5次读磁盘，插入和删除比查找多一次写磁盘。如果需要节点的分裂或归并至多再需要4次写磁盘。但分裂或归并是很少发生的，均摊到每个操作时可以忽略不计。如果让根节点常驻内存，还可减少一次I/O

外排序

大多数内排序算法都是利用了内存是直接访问的事实。如果输入是在外存储器上，随机访问某个元素将会引起一次I/O操作。外排序考虑的是尽可能减少外存访问，尽可能将每次读入的一块数据全部处理完。

在外存上进行排序的最常用的方法是利用归并排序，因为归并时只需访问归并序列中的第一个元素，非常适合于顺序文件。

外排序vs内排序

在内存中进行归并排序时，通常从规模为1的数据集合开始，逐级归并

外排序需要减少外存读写次数，因此需要尽量减少初始归并段的数量，即增加每个初始归并段的容量

外排序模型

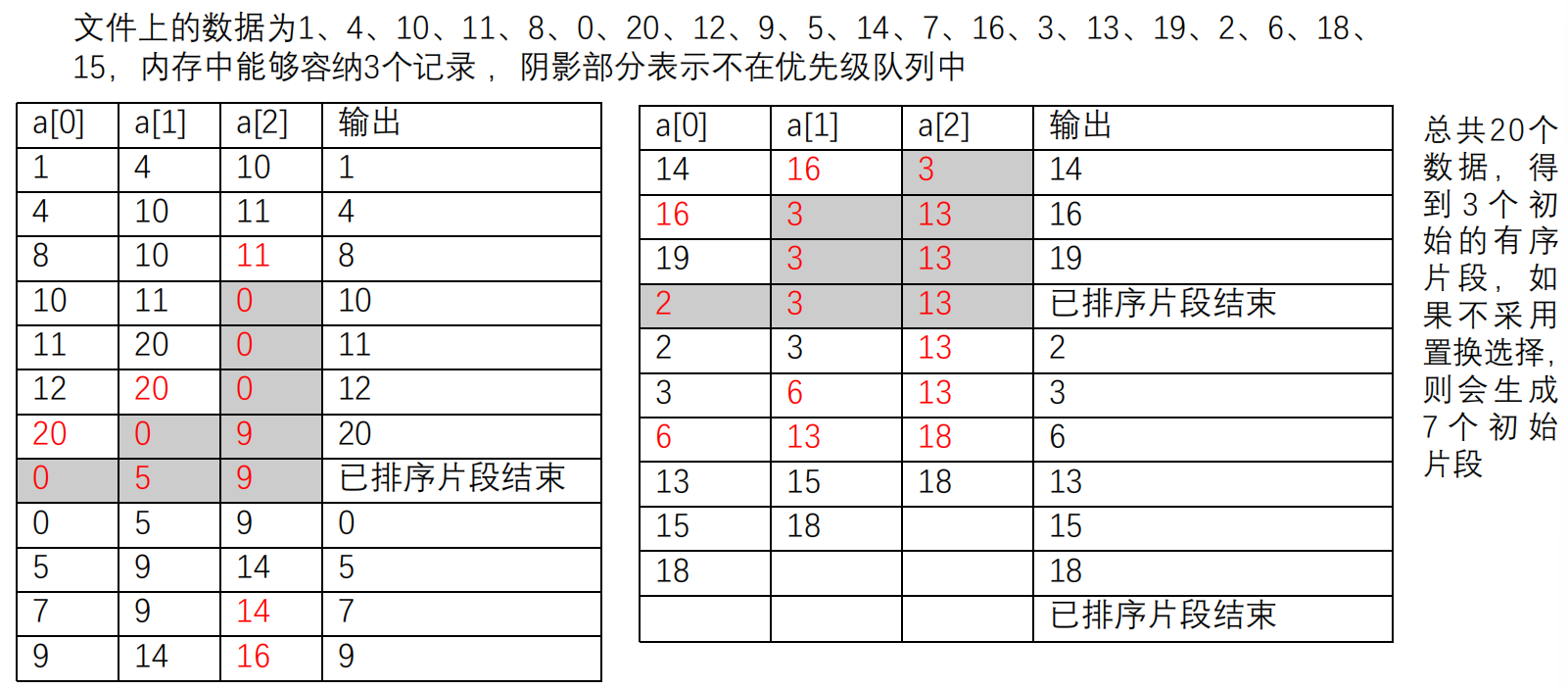
预处理阶段：根据内存的大小将一个有n个记录的文件分批读入内存，用各种内排序算法排序，形成一个个有序片段，每个片段是一个小文件。

最简单的方法：是按照内存的容量尽可能多地读入数据记录，然后在内存进行排序，排序的结果写入文件，形成一个已排序片段。

置换选择：可以在只能容纳p个记录的内存中生成平均长度为2p的初始有序片段

思想：

排序小片段时，采用选择排序（堆排序）

选出的最小元素被立即写到文件中，它所用的内存空间就可以给别的元素使用，可以从输入文件读入新元素。如果新元素比刚刚输出的元素大，它能被放入这个已排序片段，参加本次排序。

归并阶段：将这些有序片段逐步归并成一个有序文件

两路归并

多路归并（减少归并次数，但归并时找最小元素的操作复杂，通常可以将每个文件的第一个记录组成一个优先级队列）。最佳归并树：用置换选择得到的初始归并段长度不一致，在k路归并时有序段的不同组合会导致读写次数不同，采用类似哈夫曼树的归并策略

磁带上的多路归并：

k路归并需要2k条磁带
过程 (k=2)
	1. 假设初始数据在A1
	2. 从A1读入数据，形成一个个已排序片段并轮流存放在B1和B2
	3. 回绕所有磁带，重复以下过程至B1和B2为空
		• 取B1和B2上第一个已排序片段，合并后写入A1
		• 取B1和B2上下一个已排序片段，合并后写入A2
	4. 回绕所有磁带，重复以下过程至A1和A2为空
		• 取A1和A2上第一个已排序片段，合并后写入B1
		• 取A1和A2上下一个已排序片段，合并后写入B2
	5. 重复3和4直到全部排序完毕

多阶段归并：

解决磁带归并问题

磁带上的K路归并策略需要用2K条磁带，这可能限制了它在某些应用中的使用

可以仅用K+1根磁带实现K路归并

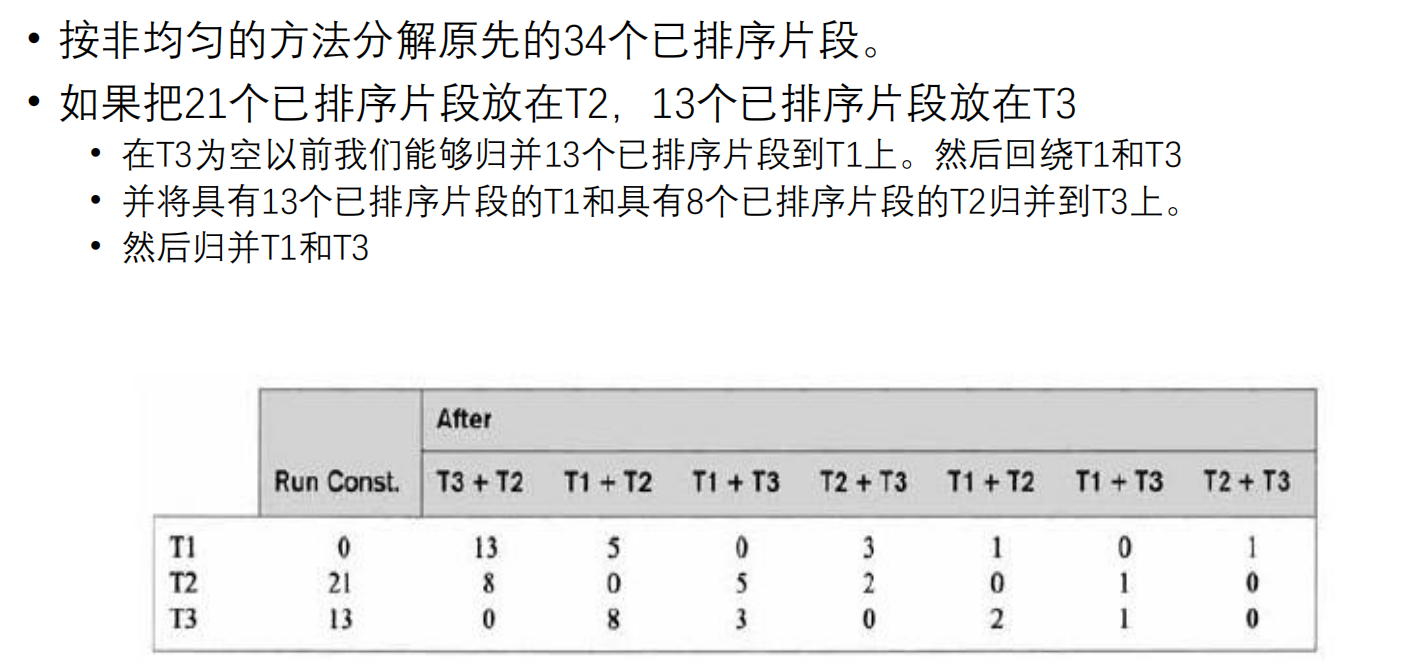
直观的方法：假设有三条磁带：T1,T2和T3 ，以及一个在T1上的输入文件，它能产生34个已排序片段。在T2和T3上各放17个已排序片段，然后把结果归并到T1。再把其中的一部分放到T2上以执行另一次归并。

如何分布初始片段：如果已排序片段的数目是一个斐波纳契数 $F_N$ ，那么分布最好的方法把它们分解成两个斐波纳契数 $F_{N-1}$ 和 $F_{N-2}$ ，否则，为了将已排序片段数增加到一个斐波纳契数，必须在磁带上填充虚拟的已排序片段。

频繁元素

频繁元素是指输入数据中有些元素会出现多次，希望找到出现最频繁的t个

Misra-Gries算法是一种计算频繁元素的近似算法，该算法需要事先规定计数器的最大数量k，即只在内存中保留k个计数器。当有数据输入时，检查是否已经为其分配了计数器，这时共有三种不同的情况需要处理：

1）有对应的计数器，则相应的计数器加1

2）没有相应的计数器，并且已有的计数器数量小于k，则为该数据分配一个新的计数器，其值设为1。

3）没有相应的计数器，并且已经有了k个计数器，则将所有的计数器数值减1，并删除值为0的计数器，新数据也被丢弃。

24 不相交集

等价关系

存储：1.二维数组 2.等价类

不相交集（并查集）

oiwiki

摘自算法笔记：

$\pi(x)$ 表示 $x$ 的父亲， $rank(x)$ 表示其下悬挂的子树的高度。

一些性质：

改进并查集：

均摊复杂度降至 $O(1)$

不相交集的应用

迷宫生成

开始时假设所有的地方都有墙（除了入口和出口），所有的单元都不连通。

我们不断地随机选择一堵墙，如果由该墙分割的单元互相之间没有连通，则把墙拆除。

重复上述过程，直到连通了入口和出口，就得到了一个迷宫。

最近共同祖先（LCA）

用后序遍历加上不相交集共同完成

将每一棵子树看成是一个等价类，子树的根是等价类的标志。

按后序遍历这棵树，在后序遍历的过程中计算每个节点的等价类，即归并其所有儿子表示的等价类和它本身。每次生成一个新的等价类后，检查节点对中的两个节点是否在一个等价类中。如果在，这个等价类的标志就是他们的共同祖先。

25 图

图的定义

图的存储

邻接矩阵、邻接表（这里好像说的是链式前向星）、逆邻接表（将进入同一节点的边组织成一个单链表）

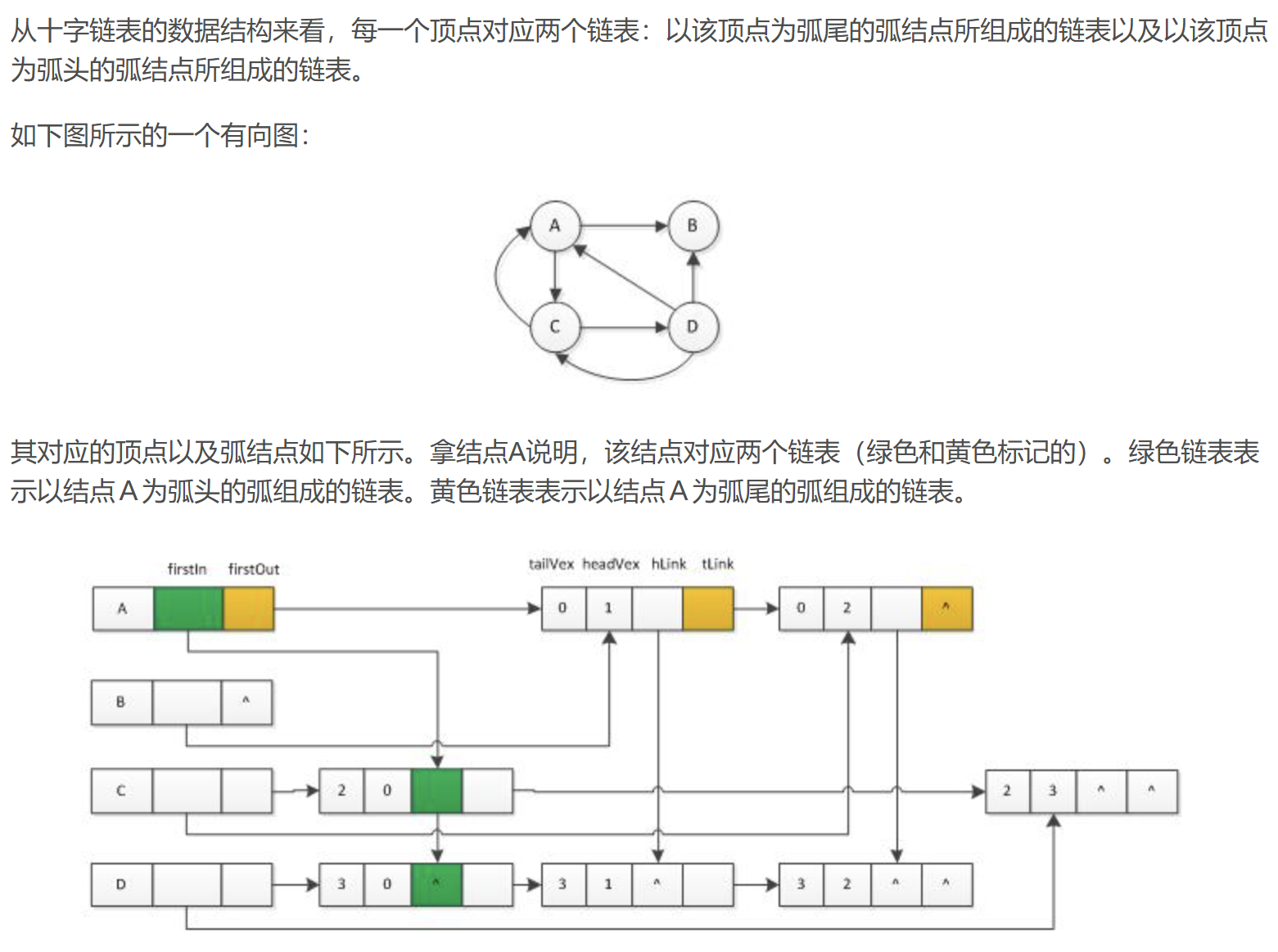
十字链表：

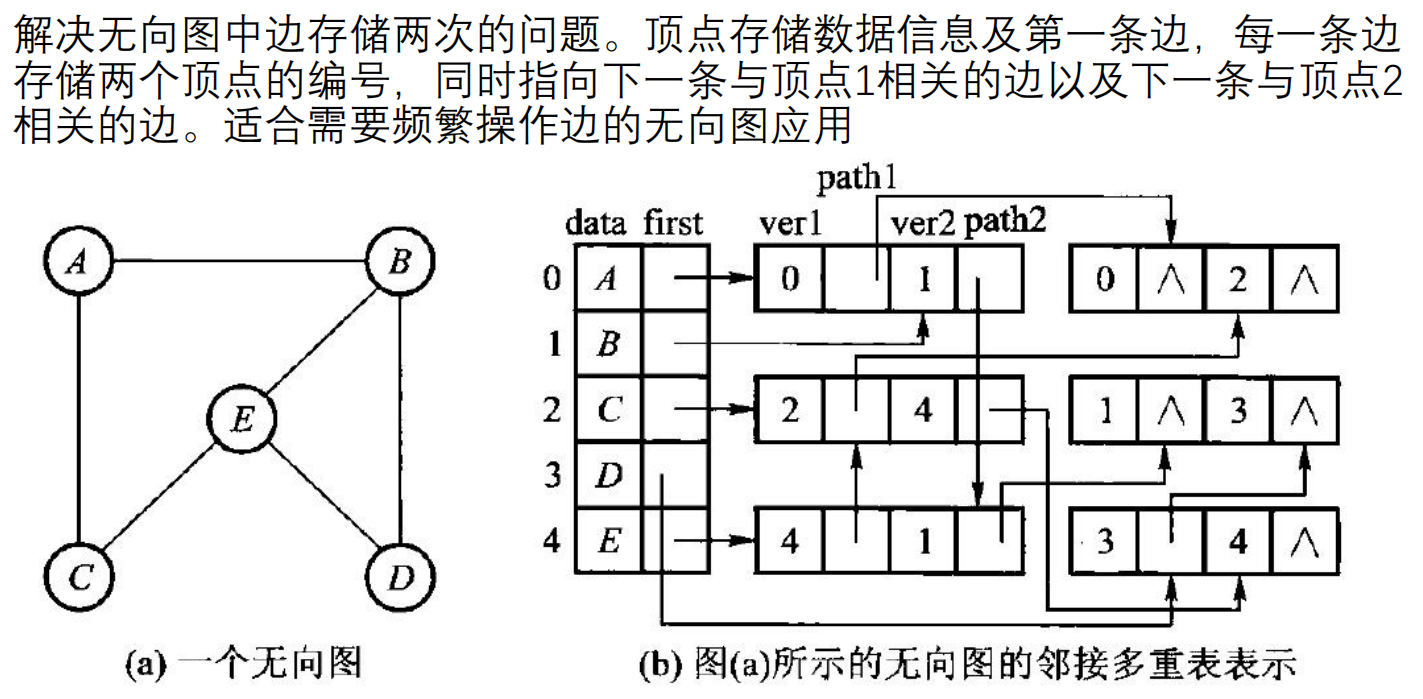
邻接多重表：考到再说吧（）

图的便历

DFS、BFS

图便历的应用

无向图的连通性

节点之间的连通

欧拉回路

欧拉路径：图中的一条路径，使得该路径对图的每一条边正好经过一次

欧拉回路：起点和终点是相同的欧拉路径

存在性？每个点的度数均为偶数

怎么找？执行一次深度优先的搜索。从起始节点开始，沿着这条路一直往下走，直到无路可走。而且在此过程中不允许回溯

路径上是否有一个尚有未访问的边的顶点。如果有，开始另一次深度优先的搜索，将得到的遍历序列拼接到原来的序列中，直到所有的边都已被访问。

实现：在邻接表类中增加一个公有成员函数EulerCircuit

欧拉回路是由一段一段的路径拼接起来的。为此，设计了一个私有的成员函数EulerCircuit来获得一段回路。

如何控制每条路只能走一遍：当一条边被访问以后，就将这条边删除。Clone函数创建一份邻接表的拷贝，以便在找完路径后能恢复这个图的邻接表

template <class TypeOfVer, class TypeOfEdge>
    void adjListGraph<TypeOfVer, TypeOfEdge>::EulerCircuit (TypeOfVer start){
        EulerNode *beg, *end, *p, *q, *tb, *te;
        int numOfDegree;
        edgeNode *r;
        verNode *tmp;
        //检查是否存在欧拉回路
        for (int i=0; i<Vers; ++i) {
            numOfDegree = 0; r = verList[i].head;
            while (r != nullptr) { ++numOfDegree; r= r->next; }
            if (numOfDegree ==0 || numOfDegree % 2) {
                cout << "不存在欧拉回路" << endl; return;
            }
        }
        i = find(start); //寻找起始节点的编号
        tmp = clone(); //创建一份邻接表的拷贝
        //寻找从i出发的路径，路径的起点和终点地址分别是beg和end
        EulerCircuit(i, beg, end);
        while (true) {
            p = beg;
            while (p->next != nullptr) //检查p的后继节点是否有边尚未被访问
                if (verList[p->next->NodeNum].head != nullptr) break;
            else p = p->next;
            if (p->next == nullptr) break; //所有的边都已被访问
            q = p->next; //尚有未被访问边的节点
            EulerCircuit(q->NodeNum, tb, te); //从此节点开始找一段回路
            te->next =q->next; //将搜索到的路径拼接到原来的路径上
            p->next = tb;
            delete q;
        }
        //恢复原图
        delete [] verList;
        verList = tmp;
        //显示得到的欧拉回路
        cout << “欧拉回路是：” << endl;
        while (beg !=nullptr) {
            cout << verList[beg->NodeNum].ver << '\t';
            p = beg;
            beg = beg->next;
            delete p;
        }
        cout << endl;
    }

template <class TypeOfVer, class TypeOfEdge>
    adjListGraph<TypeOfVer, TypeOfEdge>::verNode * adjListGraph<TypeOfVer, TypeOfEdge>::clone( ) const{
        verNode *tmp = new verNode[Vers];
        edgeNode *p;
        for (int i = 0; i < Vers; ++i) {
            tmp[i].ver = verList[i].ver;
            p = verList[i].head;
            while (p != nullptr) {
                tmp[i].head = new edgeNode(p->end, p->weight, tmp[i].head);
                p = p->next;
            }
        }
        return tmp;
    }

template <class TypeOfVer, class TypeOfEdge>
    void adjListGraph<TypeOfVer, TypeOfEdge>::EulerCircuit(int start, EulerNode *&beg, EulerNode *&end){
        //通过DFS找到一条路径
        int nextNode;
        beg = end = new EulerNode(start); //将起始节点放入欧拉回路
        while(verList[start].head != nullptr) { //起始节点尚有边未被访问
            nextNode = verList[start].head->end;
            remove(start, nextNode); //无向图的边存储两份，所以两次删除
            remove(nextNode, start);
            start = nextNode;
            end->next = new EulerNode(start);
            end = end->next;
        }
    }

有向图的连通性

环路

从图的每个节点出发进行一次一笔画，如果在一笔画的过程中遇到了已经访问过的节点，则表示出现了环。基于DFS实现。

求强连通分量（Kosaraju 算法）：

以下内容摘自算法笔记：

性质1 如果explore子过程从顶点u开始，那么该子过程恰好在从u可达的所有顶点都已访问之时终止。

因此，若我们对位于汇强连通分量（即在元图中表现为汇点的强连通分量）中的某个节点调用EXPLORE，就能获取该分量。

性质2 在深度优先搜索中得到的post值最大的顶点一定位于一个源点强连通部件中。

所以我们只需要把整个图反向， $G \Rightarrow G^R$ ，就可以在 $G^R$ 中使用 DFS 得到 $G^R$ 中post最大的，这个点在 $G^R$ 的源点强连通部件中，也就一定在 $G$ 的汇点强连通部件中。

性质3 如果 $C$ 和 $C^′$ 是强连通部件，同时从 $C$ 中的一个顶点到 $C^′$ 中的一个顶点存在一条边，则 $C$ 中post的最大值要大于 $C^′$ 中post的最大值。

于是我们得到一个最终算法：

1.在图G^ R上运行深度优先搜索。\\ 2.在图G上运行无向图连通部件算法(见3.2.3节),\\在深度优先搜索的过程中， 按照step1得到的顶点post值的降序逐个处理每个顶点。

理解： $G^R$ 中找post最大的，用这个点 EXPLORE 得到 $G$ 的汇点连通分量，然后扔掉这个分量，找剩下的图中post最大的，再用 EXPLORE …

template <class TypeOfVer, class TypeOfEdge>
    void adjListGraph<TypeOfVer, TypeOfEdge>::findStrong() const {
        int *visited=new int[Vers], seqNo=0, noOfStrong, i;
        for(i=0; i<Vers; i++) 
            visited[i]=-1;
        for(i=0; i<Vers; i++) 
            if(visited[i]<0) 
                findSeqNo(i, visited, seqNo); //给节点编号
        //生成Gr
        verNode *tmpV=new verNode[Vers]; //存放Gr的邻接表
        edgeNode *oldp, *newp;
        for(i=0; i<Vers; i++) {
            oldp=verList[i].head;
            while(oldp!=nullptr) { //遍历每条边，反向存入tmpV
                tmpV[oldp->end].head=new edgeNode(i,oldp->weight,tmpV[old->end].end);
                oldp=oldp->next; } }
        //按序号从大到小遍历Gr，输出所有强连通分量
        noOfStrong=0;
        for(seqNo=Vers-1; seqNo>=0; --seqNo) {
            for(i=0; i<Vers;++i) if(visited[i]==seqNo) break;
            if(i==Vers) continue;
            ++noOfstrong;
            cout<<endl<<“第”<<noOfStrong<<“个强连通分量: ”;
            finddfs(i, tmpV, visited);
        }
        //释放Gr
        for(i=0; i<Vers; i++) {
            oldp=tmpV[i].head;
            while(oldp!=nullptr) { newp=oldp; oldp=old->next; delete newp; }
        }
        delete []tmpV;
    }  


template <class TypeOfVer, class TypeOfEdge>
    void adjListGraph<TypeOfVer, TypeOfEdge>::findSeqNo(int start, int visited[], int &seqNo) const
        //visited的作用是记录节点是否被访问过同时用于记录后序遍历生成树时节点的序号
    {
        edgeNode *p=verList[start].head;
        visited[start]=-2; //表示下面先DFS该节点的每一个后继节点
        while(p!=nullptr){
            if(visited[p->end] == -1) findSeqNo(p->end, visited, seqNo);
            //只有-1才表示该节点未被访问过
            p=p->next;
        }
        visited[start]=seqNo++; //记录后序遍历生成树时节点的序号
    }
template <class TypeOfVer, class TypeOfEdge>
    void adjListGraph <TypeOfVer, TypeOfEdge>::finddfs(int start, verNode *tmpV, int visited[]) const{
        edgeNode *p=tmpV[start].head;
        cout<<verList[start].ver<<‘\t’;
        visited[start]=-1;
        while(p!=nullptr) {
            if(visited[p->end]!=-1) finddfs(p->end,tmpV,visited);
            p=p->next;
        }
    }

拓扑排序

基于BFS的拓扑排序：

计算每个节点的入度，保存在数组inDegree中；

检查inDegree中的每个元素，将入度为0的节点入队；

不断从队列中将入度为0的节点出队，输出此节点，并将该节点的后继节点的入度减1；如果某个邻接点的入度为0，则将其入队。

template <class TypeOfVer, class TypeOfEdge>
    void adjListGraph<TypeOfVer, TypeOfEdge>::topSort( ) const{ 
        linkQueue<int> q;
        edgeNode *p;
        int current, *inDegree = new int[Vers];
        for (int i = 0; i < Vers; ++i) inDegree[i] = 0;
        for ( i = 0; i < Vers; ++i) //计算每个节点的入度
            for (p = verList[i].head; p != nullptr; p = p->next) ++inDegree[p->end];
        for (i = 0; i < Vers; ++i) if (inDegree[i] == 0) q.enQueue(i); //入度为0的点入队
        cout << "拓扑排序为：" << endl;
        while( !q.isEmpty( ) ) {
            current = q.deQueue( ); cout << verList[current].ver << '\t';
            for (p = verList[current].head; p != nullptr; p = p->next)
                if( --inDegree[p->end] == 0 ) q.enQueue( p->end );
        }
        cout << endl;
    }

基于DFS的拓扑排序：

template<class TypeOfVer, class TypeOfEdge>
    void adjListGraph<TypeOfVer, TypeOfEdge>::topSort(int start bool visited[]) const{
        edge node *p=verList[start].head;
        visited[start]=true;
        while(p!=nullptr) {
            if(!visited[p->end])
                topSort(p->end,visited);
            p=p->next;
        }
        cout<<verList[start].ver<<‘\t’;
    }

分组拓扑排序

由于课程之间有先导关系，因此如何安排培养计划，使得能够用最少的学期数修完所有的课程

双队列，当前入度为0的顶点都进入队列q1，然后将q1中的点依次出队列，同时将其后继节点的入度减1，若后继节点入度为0，则进入队列q2。接着类似处理队列q2，将q2中的点依次出队列，同时将其后继节点的入度减1，若后继节点入度为0，则进入队列q1。重复以上过程直至所有点都处理完。

AOV和AOE网络

AOV(activity on vertex) 网络：有向无环图

顶点表示活动，边表示活动的先后次序。主要应用：安排活动的顺序，即拓扑排序

AOE(activity on edge)网络：加权有向无环图

顶点表示事件，有向边的权值表示某个活动的持续时间，有向边的方向表示活动和事件的先后次序，进入顶点的所有活动都结束后，顶点表示的事件发生了，从该顶点出发的所有活动可以开始了

关键路径

完成整项工程至少需要多少时间：源点到汇点的最长路径的长度，该路径称为关键路径。关键路径可能有多条

哪些活动是影响工程进度的关键：加快这些活动可以缩短工期，耽误这些活动则会延长工期

影响工期的活动称为关键活动。

找出每个顶点的最早发生时间和最迟发生时间

最早发生时间：前面的活动都没有耽误时间，这个事件的发生时间
最迟发生时间：不影响整个项目按时完成的前提下，这个事件最晚可以什么时候发生

最早发生时间和最晚发生时间相同的顶点序列构成关键路径

找出拓扑序列
从头到尾遍历拓扑序列找出节点最早发生时间
从尾到头遍历拓扑序列找到最迟发生时间
从头到尾遍历拓扑序列，找出最早发生时间和最迟发生时间相等的顶点组成关键路径。

template <class TypeOfVer, class TypeOfEdge>
    void adjListGraph<TypeOfVer, TypeOfEdge> ::criticalPath( ) const
    {
        TypeOfEdge *ee = new TypeOfEdge[Vers], *le = new TypeOfEdge[Vers];
        int *top = new int[Vers]; //拓扑序列
        int *inDegree = new int[Vers];
        linkQueue<int> q;
        int i;
        edgeNode *p;
        // 找出拓扑序列，放入数组top
        for (i = 0; i < Vers; ++i) inDegree[i] = 0;
        for (i = 0; i < Vers; ++i) { //计算每个节点的入度
            for (p = verList[i].head; p != nullptr; p = p->next)
                ++inDegree[p->end];
        }
        for (i = 0; i < Vers; ++i) //将入度为0的节点入队
            if (inDegree[i] == 0) q.enQueue(i);
        i = 0;
        while( !q.isEmpty( ) ) {
            top[i] = q.deQueue( );
            for (p = verList[top[i]].head; p != nullptr; p = p->next)
                if( --inDegree[p->end] == 0 ) q.enQueue( p->end );
            ++i;
        }
        // 找最早发生时间
        for (i = 0; i < Vers; ++i) ee[i] = 0;
        for (i = 0; i < Vers; ++i)
            for (p = verList[top[i]].head; p != nullptr; p = p->next)
                if (ee[p->end] < ee[top[i]] + p->weight ) ee[p->end] = ee[top[i]] + p->weight;
        // 找最晚发生时间
        for (i = 0; i < Vers; ++i) le[i] = ee[top[Vers -1]];
        for (i = Vers - 1; i >= 0 ; --i)
            for (p = verList[top[i]].head; p != nullptr; p = p->next)
                if(le[p->end] - p->weight < le[top[i]] ) le[top[i]] = le[p->end] - p->weight;
        // 找出关键路径
        for (i = 0; i < Vers; ++i)
            if (le[top[i]] == ee[top[i]])
                cout << "(" << verList[top[i]].ver << ", " << ee[top[i]] << ") ";
    }

26 最小生成树贪心算法矩阵

最小生成树

拟阵

定义:给定一个无向图 G=(V,E)，图拟阵 M(G)的基础集是边集 E，其独立集族是所有不包含
环的边集，即所有的森林。

独立集族中的最大独立集就是生成树。

下面同样的，我们把算法笔记粘贴过来。

一个贪心方法

形式化：

Kruskal算法：不断重复地选择未被选中的边中权重最轻且不会形成环的一条。

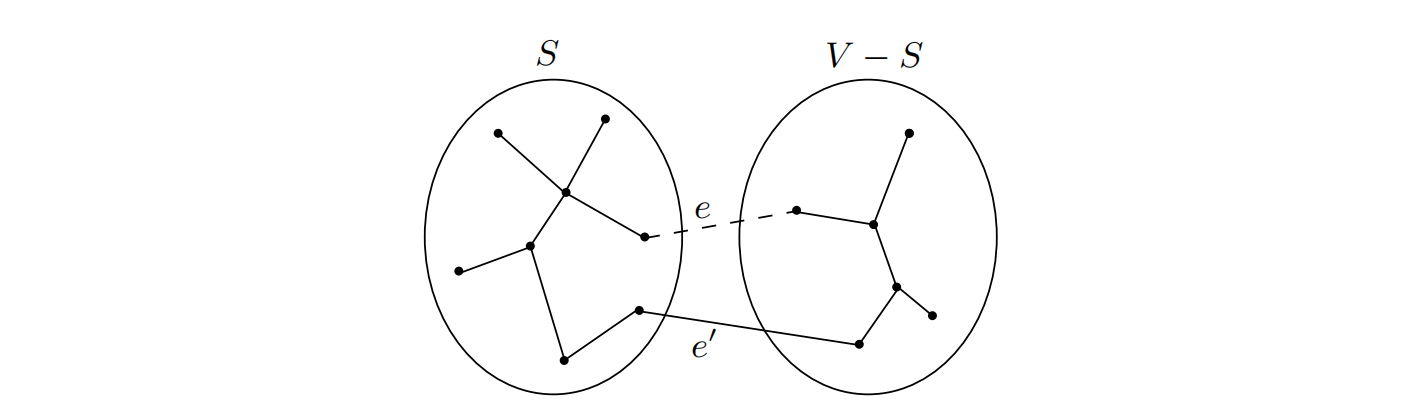
分割性质

Kruskal算法的正确性由分割性质（Cut property）保证。

证明：

T是MST，若不包含 $e$ ，由于连通，一定包含 $e'$ ，则把 $e'$ 换成 $e$ 之后得到的 $T'$ 边权小于等于 $T$ 。所以一定等于 $\Rightarrow$ $T'$ 也是MST。

Kruskal 算法

Prim 算法

（Kruskal算法的变体）

上面几种算法的具体代码实现可以见 Slides 或者 oiwiki

27 模块

课件： 1 2

模块接口文件

所有C++头文件都是所谓的可导入头文件，可通过import导入

//person.cppm 接口文件
export module person; //module declaration
import <string>; //import declaration
export class Person //export declaration
{...};

//test.cpp
import person; //import declaration for person module
import <iostream>;
import <string>; // For operator<< for std::string
using namespace std;
int main(){
    Person person{ "Kole", "Webb" };
    cout << person.getLastName() << ", " << person.getFirstName() << endl;
}

全局模块

以匿名模块的声明开始，只包含include等预处理指令。这样的全局模块是唯一允许出现在命名模块声明之前的内容

//person.cppm
module; //start of the global module fragment
#include <cstddef> //include legacy header files
export module person; //module declaration
import <string>; //import declaration
export class Person //export declaration
{......};

//导出命名空间
export namespace DataModel
{
    class Person { /* ... */ };
    class Address { /* ... */ };
    using Persons = std::vector<Person>;
}//使用：DataModel::Person p

//导出整个声明块
export //注意此处和前一页的区别
{
    namespace DataModel
    {
        class Person { /* ... */ };
        class Address { /* ... */ };
        using Persons = std::vector<Person>;
    }
}//使用：DataModel::Person p

从命名模块声明到文件末尾的所有内容称为模块作用域，通过export控制哪些内容对外可见，哪些内容保持模块私有

接口与实现分离

一种方法是在模块接口文件中拆分接口和实现，另一种方式是将模块拆分为接口文件和实现文件

在一个文件中拆分实现：

//Person.cppm
export module person;
import <string>;
// Class definition
export class Person
{
    public:
    Person(std::string firstName, std::string lastName);
};
// Implementations, but the same file
Person::Person(std::string firstName, std::string lastName)
    : m_firstName{ std::move(firstName) }, m_lastName{ std::move(lastName) }
{ ... }

下面的部分没有export，无法导出，隐藏，仅做实现

分两个（模块实现文件）：

//Person.cppm
export module person;
import <string>;
export class Person {
    public:
    Person(std::string firstName, std::string lastName);
};

//Person.cpp
//模块实现文件包含一个已命名模块的声明，用于指定实现所针对的模块
module person;//隐式包含import person，但不会继承person模块所import的内容，如string（这一点对于所有使用的时候的情况都是一样的）如果用到了模块中的函数，这个函数使用了string，那没关系，但是如果要直接使用string，不可以
using namespace std;
Person::Person(string firstName, string lastName)
    : m_firstName{ move(firstName) }, m_lastName{ move(lastName) }
{ ... }

模块接口和模块实现文件的所有导入声明必需位于文件的开始，在已命名模块声明之后，在其它任何声明之前，模块实现文件不能导出任何内容，只有模块接口文件可以

子模块与模块分区

子模块（点号）：

用户可以一次导入他们想要使用的模块特定部分或全部内容

//之前的模块接口
export module model;
export namespace Datamodel{
    class Person {...};
    class Address {...};
    ... 
}
//子模块datamodel.person的模块接口文件
export module datamodel.person;
export namespace DataModel { class Person {...}; }
//子模块datamodel.address的接口文件
export module datamodel.address;
export namespace DataModel { class Address {...}; }

//模块datamodel的接口文件
export module datamodel;
export import datamodel.person; //导入并立即导出
export import datamodel.address;

//用户代码
//用户只需使用类Address
import datamodel.address;
//用户需要使用所有内容
import datamodel;

也就是说，我写了一个datamodel.person.cppm和datamodel.address.cppm，

本来我需要使用的时候导入两次，现在我用一个datamodel.cppm集成（在这个文件里写export module datamodel; export import datamodel.person; export import datamodel.address;），

然后在使用的时候既可以import datamodel.address;也可以import datamodel;

子模块的构造对用户可见，用户可以选择导入需要的子模块

模块分区（冒号）：

分区用于内部构造模块，不对用户公开。在模块接口分区文件中声明的所有分区，最终必须由(包含导出模块名称声明的)主模块接口文件导出

可以将分区的实现放在主模块实现文件中

多个文件不能具有相同的分区名称，不能存在多个具有相同分区名的模块接口分区文件。模块接口分区文件中的声明不能在具有相同分区名的实现文件中实现，而是放在模块的实现文件中

//datamodel.cppm
export module datamodel; // datamodel module (primary module interface file)
export import :person; // Import and export person partition
export import :address; // Import and export address partition
export namespace DataModel { using Persons = std::vector<Person>; }

//datamodel.address.cppm
export module datamodel:address; // datamodel:address partition
export namespace DataModel {
    class Address { public: Address(); };
}

//datamodel.person.cppm
export module datamodel:person; // datamodel:person partition
export namespace DataModel {
    class Person { /* ... */ };
}

//datamodel.address.cpp
module datamodel; // Not datamodel:address!
import <iostream>;
using namespace std;
DataModel::Address::Address() {
    cout << "Address::Address()" << endl;
}

//demo.cpp
import datamodel; //不能导入单个分区
int main() { DataModel::Address a; }

模块分区=组织内的部门分类，

每个 “部门”（分区）只能属于一个 “组织”（主模块），不能独立存在或加入其他组织。

子模块=子模块就像是人的所属，可以既属于这个组织也属于那个组织

一个 “成员”（子模块）可以同时属于多个 “组织”（主模块），甚至独立存在。
每个组织可以选择是否 “引入” 该成员，且成员有独立的 “身份标识”（命名空间）。

实现分区/内部分区

在模块的实现文件中声明的分区，通常包含了其它实现文件都需使用的辅助函数，但是不能被导出

//math.cppm
export module math; // math module declaration
export namespace Math {
    double superLog(double z, double b);
    double lerchZeta(double lambda, double alpha, double s);
}

//math.cpp
module math;
import :details;
double Math::superLog(double z, double b) {
    return someHelperFunction(z); // Implementation omitted... 
}
double Math::lerchZeta(double lambda, double alpha, double s) {
    return someHelperFunction(s); // Implementation omitted... 
}

//math_helpers.cpp
module math:details;
// math:details implementation partition
double someHelperFunction(double a) {
    // Implementation omitted... return 42;
}

28 模板与概念

PDF

类模板

不使用模板：将类的一些数据成员的类型，方法的返回类型，方法的参数类型指定为参数

//采用多态，棋盘保存通用的GamePiece对象
export class GamePiece {
    public:
    virtual ~GamePiece() = default;
    virtual std::unique_ptr<GamePiece> clone() const = 0;
};
//每种游戏的棋子继承GamePiece
class ChessPiece : public GamePiece {
    public:
    std::unique_ptr<GamePiece> clone() const override{
        // Call the copy constructor to copy this instance
        return std::make_unique<ChessPiece>(*this);
    }
};

方法模板：

可以再次模板化普通类以及类模板中的单个方法，虚方法和析构函数除外

带有非类型参数的方法模板：eg.可以将不同高度和宽度的Grid进行拷贝构造/赋值，不一定要把源对象完美复制到目标对象，一方面可以从源对象中只复制那些能够被放入目标对象的元素，另一方面，如果源对象在某个维度上小于目标对象，可以用默认值进行填充

类模板的特化

编写类模板的特化时，必须指明这是一个模板以及为哪种特定类型编写这个模板

为const char*特化的Grid实现中，初始的Grid模板放置在main模块接口分区中，特化部分放置在string模块接口分区

//Grid.cppm 模块接口文件
export module grid;
export import :main;
export import :string;

特化与派生不同，不继承任何代码，需要重新编写类的所有实现，不要求提供具有相同的名称或行为的方法。每个方法定义之前不必写template<>

//GridString.cppm
export module grid:string;
// When the template specialization is used, the original template must be visible too. import :main; //原来的Grid类模板假设在一个名为main的模块接口文件
export template <> //告诉编译器这是Grid的const char*特化版本，不指定任何类型参数，但是这一行不能少
class Grid<const char*> {...}

//不需要template<>，因为类型已经被特化死了
Grid<const char*>::Grid(size_t width, size_t height) : m_width{ width }, m_height{ height } {
    m_cells.resize(m_width);
    for (auto& column : m_cells) column.resize(m_height);
}

从类模板派生：

//GameBoard.cppm
import grid;
export template <typename T>
class GameBoard : public Grid<T> {
	...
};
template <typename T>
void GameBoard<T>::move(size_t xSrc, size_t ySrc, size_t xDest, size_t yDest) {
    //使用this或Grid<T>::来指明基类模板中的数据成员和方法
    Grid<T>::at(xDest, yDest) = std::move(Grid<T>::at(xSrc, ySrc));
    Grid<T>::at(xSrc, ySrc).reset(); // Reset source cell
    // this->at(xDest, yDest) = std::move(this->at(xSrc, ySrc));
    // this->at(xSrc, ySrc).reset();
}

模板别名：

//假设有如下类模板
template<typename T1, typename T2>
class MyTemplateClass {...};
//可以给定两个类型参数来定义别名
using OtherName=MyTemplateClass<int, double>;//可以用typedef
//还可以指定部分类型，这又称为别名模板
template<typename T1>
using otherName=MyTemplateClass<T1, double>; //此时不能用typedef

函数模板

可以的用法以及不可以的用法：

static const size_t NOT_FOUND{ static_cast<size_t>(-1) };
template <typename T>
size_t Find(const T& value, const T* arr, size_t size){
    for (size_t i{ 0 }; i < size; i++) {
        if (arr[i] == value) {
            return i; // Found it; 
            return the index. 
        }
    }
    return NOT_FOUND; // Failed to find it; 
    return NOT_FOUND. 
}
int main() {
    int myInt{ 3 }, intArray[]{ 1, 2, 3, 4 };
    const size_t sizeIntArray{ size(intArray) };
    size_t res;
    res = Find(myInt, intArray, sizeIntArray); // calls Find<int> by deduction. 
    res = Find<int>(myInt, intArray, sizeIntArray); // calls Find<int> explicitly. if (res != NOT_FOUND) { cout << res << endl; }
    else { cout << "Not found" << endl; }
    double myDouble{ 5.6 }, doubleArray[]{ 1.2, 3.4, 5.7, 7.5 };
    const size_t sizeDoubleArray{ size(doubleArray) };
    res = Find(myDouble, doubleArray, sizeDoubleArray); // calls Find<double> by deduction. 
    res = Find<double>(myDouble, doubleArray, sizeDoubleArray); // calls Find<double> explicitly. 
    if (res != NOT_FOUND) { cout << res << endl; }
    else { cout << "Not found" << endl; }
    res = Find(myInt, doubleArray, sizeDoubleArray); // 错误。DOES NOT COMPILE! Arguments are different types. 
    res = Find<double>(myInt, doubleArray, sizeDoubleArray); // calls Find<double> explicitly, even with myInt. 
    SpreadsheetCell cell1{ 10 };
    SpreadsheetCell cellArray[]{ SpreadsheetCell{ 4 }, SpreadsheetCell{ 10 } };
    const size_t sizeCellArray{ size(cellArray) };
    res = Find(cell1, cellArray, sizeCellArray); // calls Find<SpreadsheetCell> by deduction. 
    res = Find<SpreadsheetCell>(cell1, cellArray, sizeCellArray); // calls Find<SpreadsheetCell> explicitly. 
}

函数模板的重载：

size_t Find(const char* value, const char** arr, size_t size) {
    for (size_t i{ 0 }; i < size; i++)
        if (strcmp(arr[i], value) == 0) return i; // Found it; return the index. 
    return NOT_FOUND; // Failed to find it; return NOT_FOUND. 
}

size_t res{ Find(word, words, sizeWords) }; // Calls non-template function. 
res = Find<const char*>(word, words, sizeWords); // Calls template with T=const char*.

类模板的友元函数模板

export module grid;
export template <typename T> class Grid; // Forward declare Grid template. 
export template<typename T> Grid<T> operator+(const Grid<T>& lhs, const Grid<T>& rhs);
export template <typename T>
    class Grid { public: friend Grid operator+<T>(const Grid& lhs, const Grid& rhs); //operator+<T>模板是Grid<T>的友元
......};
export template <typename T> Grid<T> operator+(const Grid<T>& lhs, const Grid<T>& rhs) {
...
}

模板参数推导：

变量模板：

概念

背景：为模板提供错误参数时，编译器给出数百行错误信息

概念（Concepts）是模板编程的重大改进，它通过约束模板参数（类型参数和非类型参数），显著提升了代码的可读性、错误信息清晰性和泛型编程的灵活性

1 2	template <parameter-list> concept concept-name=constraints-expression;

看似是模板，但我们不会把它实例化。constraints-expression可以是任意的（编译时可计算的）常量表达式，必须产生一个布尔值，运行时不会被计算。用以表示模板参数必须满足的条件

概念表达式的语法为：concept-name<argument-list>，其结果为真或假，如果为真则表示使用给定的模板实参为概念建模

约束表达式

简单requirement

是一个任意的表达式语句，不允许使用变量声明，循环，条件语句等，该表达式语句编译器只是验证是否通过编译，不会真的去做

下例概念定义指定类型T必须是可递增的，支持前缀++和后缀++运算符

1 2	template <typename T> concept Incrementable = requires(T x) { x++; ++x; }

require表达式的参数列表用于引入位于require表达式主体中的命名变量，且require表达式的主体不能有常规变量的声明

类型requirement

用于验证是否是一种特定类型

下例要求T有value_type成员

1 2	template <typename T> concept C=requires { typename T::value_type; };

类型需求可以用来验证某个模板是否可以使用给定的类型进行实例化

1 2	template <typename T> concept C = requires { typename SomeTemplate<T>; };

复合requirement

用于验证某些东西不会抛出任何异常和/或验证某个方法是否返回某个类型，下面语法格式中

noexcept和->type-constraint是可选

1	{ expression } noexcept -> type-constraint;

下例验证给定类型是否具有标记为noexcept的swap方法

1 2	template <typename T> concept C=requires(T x, T y) { { x.swap(y) } noexcept; };

下例验证给定类型是否具有一个size方法，且该方法的返回类型可转换为size_t

1 2	template <typename T> concept C=requires(const T x) { { x.size() } -> convertible_o<size_t>; };

std::convertible_to<From, to>是标准库在<concepts>中定义的概念，具有两个类型参数，->左边的表达式的类型自动作为第一个类型参数传递给convertible，此时只需指定To对应的实参（此例中为size_t）

下例要求类型T可比较

template <typename T>
concept Comparable=requires(const T a, const T b) {
    { a==b } -> convertible_o<bool>;
    { a < b } -> convertible_o<bool>;
    //以及其它比较运算
};

嵌套requirement

下例要求类型大小为4个字节，支持前缀和后缀的++与–

template <typename T>
concept C=requires (T t) {
    requires sizeof(t) == 4;
    ++t; --t; t++; t--;
};

组合：

使用&&和||对已有概念进行组合

设已经有一个Incrementable和一个Decrementable的概念，定义一个新的概念，要求一个类型既可以递增又可以递减

1 2	template <typename T> concept IncrementableAndDecrementable=Incrementable<T> && Decrementable<T>

已有的概念：

类型约束

auto的类型约束

上面的例子：用1初始化的value1能否通过Incrementable

函数模板的类型约束

两种写法：在template里面修饰或者在后面写require

约束包含

类模板的类型约束

//新的GameBoard类模板，要求模板类型参数是GamePiece的派生类
template <std::derived_from<GamePiece> T>
//或者 template <typename T> requires std::derived_from<T, GamePiece>
class GameBoard : public Grid<T> {
    ...
};
template <std::derived_from<GamePiece> T>
GameBoard<T>::GameBoard(size_t width, size_t height) : Grid<T>{ width, height } { }

//可以对类模板的特定方法添加额外的约束。例如move方法进一步要求类型T是可移动的
template <std::derived_from<GamePiece> T>
class GameBoard : public Grid<T> {
    void move(size_t xSrc, size_t ySrc, size_t xDest, size_t yDest) requires std::movable<T>;
};
//此时方法定义时也要加require
template <std::derived_from<GamePiece> T>
void GameBoard<T>::move(size_t xSrc, size_t ySrc, size_t xDest, size_t yDest) requires std::movable<T>
{ ... }
//注：基于前面讨论的选择性实例化，仍然可以使用非移动类型的GameBoard，只要不使用其move方法

模板特化的类型约束

//可以为类模板编写特化，可以重载函数模板使特定类型有特定实现，还可以一类满足特定条件的类型进行特化，以下是常规的Find函数模板
template <typename T>
size_t Find(const T& value, const T* arr, size_t size) {
    for (size_t i{ 0 }; i < size; i++) if (arr[i] == value) return i; // Found it; return the index. 
    return NOT_FOUND; // Failed to find it; 
} 
//该模板使用==进行比较，但对于浮点数，这种方式不太合适，为此进行特化
template <std::floating_point T>
size_t Find(const T& value, const T* arr, size_t size) {
    for (size_t i{ 0 }; i < size; i++) if (AreEqual(arr[i], value)) return i; // Found it; return the index. 
    return NOT_FOUND; // Failed to find it; return NOT_FOUND. 
} 
//辅助函数模板AreEqual，也要使用类型约束
template <std::floating_point T>
bool AreEqual(T x, T y, int precision = 2) {
    return fabs(x - y) <= numeric_limits<T>::epsilon() * fabs(x + y) * precision
        || fabs(x - y) < numeric_limits<T>::min(); // The result is subnormal. 
}

practice:

29 范围

迭代器是容器之上的抽象。而范围是迭代器之上的抽象，它消除了迭代器不匹配的错误，并增加了额外的功能

范围库

基于范围的算法：

//我们熟悉的sort：
vector data {33, 11, 22 };
sort(begin(data), end(data));
//基于范围的sort：
ranges::sort(data)

投影

很多基于范围的算法都有一个所谓的投影参数，这是一个回调参数，用于在将每个元素交给算法之前对其进行转换。利用投影，可以在操作范围（如排序、查找、转换等）时，先对元素进行某种转换或提取，再基于转换后的结果进行操作。投影不会修改原始数据，它只是提供一个临时的“视角”来处理数据。

class Person {
    public: Person(string first, string last): m_firstName{ move(first) }, m_lastName{ move(last) } { }
    const string& getFirstName() const { return m_firstName; }
    const string& getLastName() const { return m_lastName; }
    private: string m_firstName;
    string m_lastName;
};
int main() {
    sort(begin(persons), end(persons)); // 错误：没有定义operator<
    ranges::sort(persons); // 错误：基于范围的ranges::sort也不能简单套用
    ranges::sort(persons, {},[](const Person& person) { return person.getFirstName(); });
    //第二个参数{}的作用是使用一个默认的比较器对象std::ranges::less，
    //第三个参数为投影参数，可以使用lamda表达式。或者下面更简洁的形式
    ranges::sort(persons, {}, &Person::getFirstName);
    
    ranges::sort(persons, ranges::greater{}, &Person::getFirstName);
    //自定义比较器（greater）
}

视图

视图是一种特殊的范围

视图允许对底层范围元素执行操作。视图可以串联/组合在一起，形成对范围元素执行多种操作的管道/流水线。具有如下特性：

惰性计算：构建视图并不会对底层范围执行任何操作。只有在遍历视图元素并取消引用迭代器时，才会应用视图的操作。
非占有：视图不拥有任何元素。顾名思义，它是对存储在某个容器中的元素范围的视图，而该容器才是数据的所有者。视图是数据的 “观察者”，它只是对现有范围的包装，只是允许你以不同的方式查看数据。因此，视图中元素的数量并不会影响复制、移动或销毁视图的成本。
非突变：创建视图不修改范围中的原始数据，能反映范围的变化，特定场合可以通过视图显式操作数据

范围适配器

过滤或者只保留部分内容

auto result1{ values | views::filter([](const auto& value) { return value % 2 == 0; }) };//留下偶数
// 或者 auto result1{ ranges::filter_view{ values, [](const auto& value) { return value % 2 == 0; } } };
auto result2{ result1 | views::transform([](const auto& value) { return value * 2.0; }) };//乘2
auto result3{ result2 | views::drop(2) }; //抛弃前两个
auto result4{ result3 | views::reverse }; //反向
//视图不修改元素
//原始数据变化，视图内容发生变化

管道/流水线模式：

printRange("Original sequence: ", values);
auto result{ values
    | views::filter([](const auto& value) { return value % 2 == 0; })
    | views::transform([](const auto& value) { return value * 2.0; })
    | views::drop(2)
    | views::reverse };
printRange("Final sequence: ", result);

通过视图修改元素：

1 2	auto result3{ result2 \| views::reverse }; for (auto& value : result3) { value *= 10; } // Modify the elements using a range-based for loop.

映射元素

auto result{ values
| views::filter([](const auto& value) {return value % 2 == 0; })
| views::take(3)
| views::transform([](const auto& v) { return format(R"("{}")", v); }) };

Result: “2” “4” “6”

范围工厂

auto values{ views::iota(10) }; //得到无穷序列10, 11, 12, ... 
auto result1{ values | views::filter([](const auto& value) {return value % 2 == 0; }) }; //得到偶数序列
auto result2{ result1 | views::transform([](const auto& value) {return value * 2.0; }) }; //乘2.0
auto result3{ result2 | views::take(10) }; //取前10个
printRange("Result: ", result3);

输入流作为视图

basic_istream_view/istream_view范围工厂可用于构建从输入流读取的元素的视图，使用>>读取元素

下面的程序从标准输入读取整数，对于每个小于5的数字，将该数字加倍并输出，输入大于等于5的数字则结束（输入非int以及EOF也会结束）

for (auto value : ranges::istream_view<int>(cin)
     | views::take_while([](const auto& v) { return v < 5; })
     | views::transform([](const auto& v) { return v * 2; })) {
    cout << format("> {}\n", value);
}

Categories

Tags

Archives

Recent Posts

15.5 平摊分析

16 栈

函数：

栈的应用：

递归函数的非递归实现

符号平衡检查

表达式的计算

17 队列

队列的应用：

列车车厢重排

排队系统的模拟

17.5 哈希

18 字符串

串匹配

KMP算法

BM算法

回文串 - Manacher算法

19 树

二叉树

二叉树的性质：

二叉树的遍历：

顺序实现与链接实现

表达式树

哈夫曼树

哈夫曼算法

哈夫曼编码

哈夫曼树

哈夫曼树类实现：

树和森林

链式前向星（孩子链表示法）

孩子兄弟链表示法

双亲表示法

森林的二叉树表示

20 优先级队列

二叉堆

排队系统的模拟

其他堆

D堆

左堆

斜堆

二项堆

优先级队列的表示

杨氏矩阵

STL中的优先级队列

21 集合与静态查找表

无序表查找

有序表查找

顺序查找

二分查找

插值查找

分块查找

STL中的静态查找表

22 动态查找表

二叉查找树

平衡二叉查找树

AVL树

插入：

删除：

伸展树（Splay树）

22-2 红黑树

22-3 文本压缩

LZW规则

LZW解压缩

23 外部查找与排序

外存储器

外部查找

B树

B+树

外排序

外排序vs内排序

外排序模型

频繁元素

24 不相交集

等价关系

不相交集（并查集）

不相交集的应用

26 最小生成树贪心算法矩阵