——smiling
用于记录算法课程的学习。
笔记中的所有图片来源于教材与陈翌佳老师的Slides。
已更新完毕(2025.6.5 最后一次算法课)
第 0 章 序言
0.1 书籍和算法
0.2 从 Fibonacci 数列开始
算法:

时间复杂度:线性
0.3 大 O 符号
第 1 章 数字的算法
1.1 基本算术
1.1.1 加法
二进制,n位
时间复杂度:
1.1.2 乘法和除法
乘法:
法一: 次加法,时间复杂度
法二:
时间复杂度
除法:

时间复杂度
1.2 模运算
1.2.1 模的加法和乘法
加法时间复杂度:
乘法时间复杂度:
除法时间复杂度:
1.2.2 模的指数运算

倍增算法,时间复杂度:
1.2.3 Euclid 的最大公因数算法

时间复杂度:
1.2.4 Euclid 算法的一种扩展

扩展欧几里得算法在给出 的同时还给出了 中的 和 。
得到获取模逆的 算法
1.2.5 模的除法
用模逆算
1.3 素性测试
费马小定理:
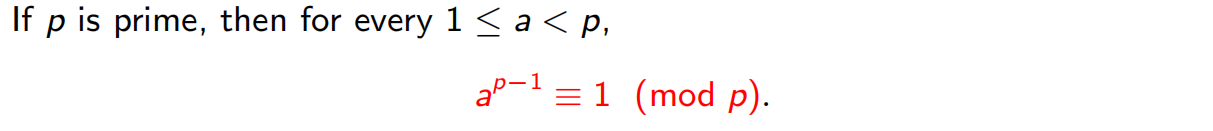
素性测试:

我们的期望:对于非素数,这个算法能够很大概率输出no
只要有一次输出no,就不是素数。
但是:
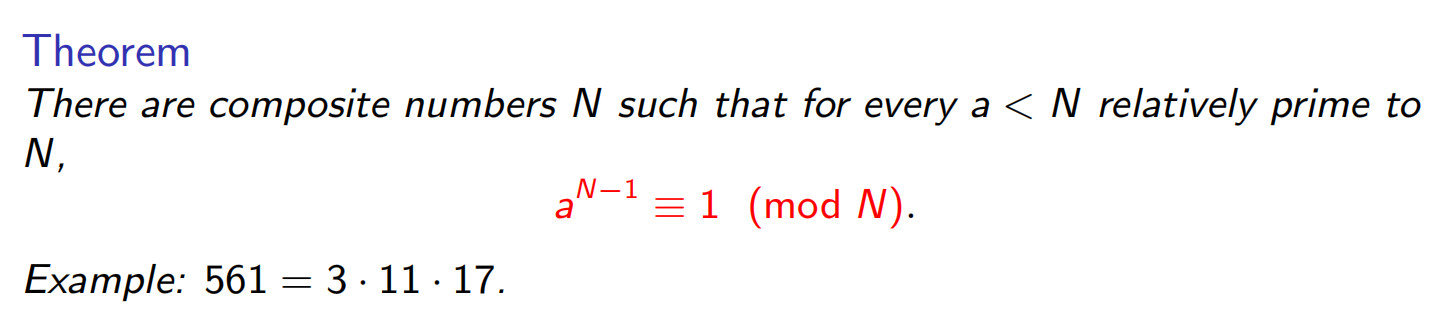
确实存在这样的合数,很大概率是yes的,称为 Carmichael numbers
对于非Carmichael numbers,我们的期望是成立的:
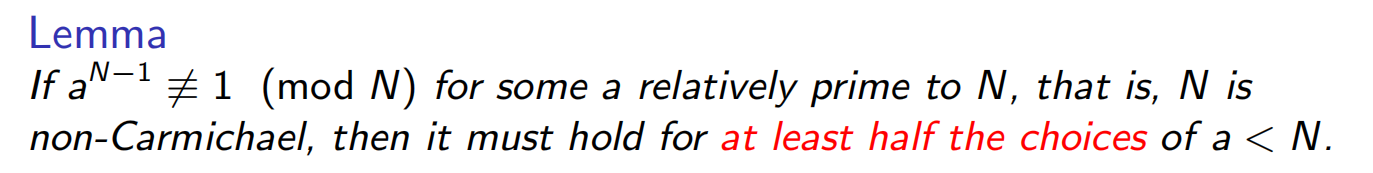
改进:一次测多个:

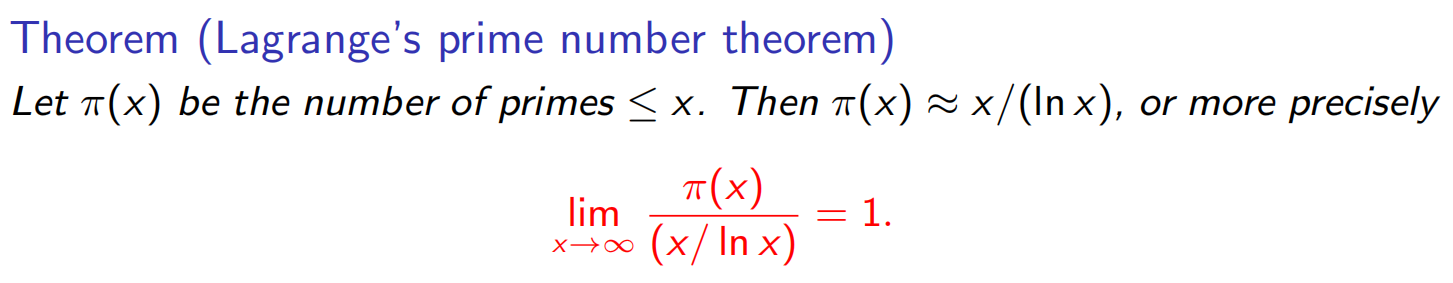
时间复杂度:平均会在 轮后停下。
1.4 密码学
1.4.1 密钥机制:一次一密乱码本和 AES
一次一密乱码本:

1.4.2 RSA
Bob给出一个公匙 ,自己保留私匙 , ,当 Alice 想给 Bob 传 的时候,她传出 , Bob通过 恢复
其中 需要满足 是 对于 的模逆。
1.5 通用散列表
1.5.1 散列表
哈希函数
目的:给一个较短的nickname给一个很长的IP地址,且使得两个IP地址nickname相同的概率(哈希碰撞概率)较小。
1.5.2 散列函数族

第 2 章 分治算法
2.1 乘法
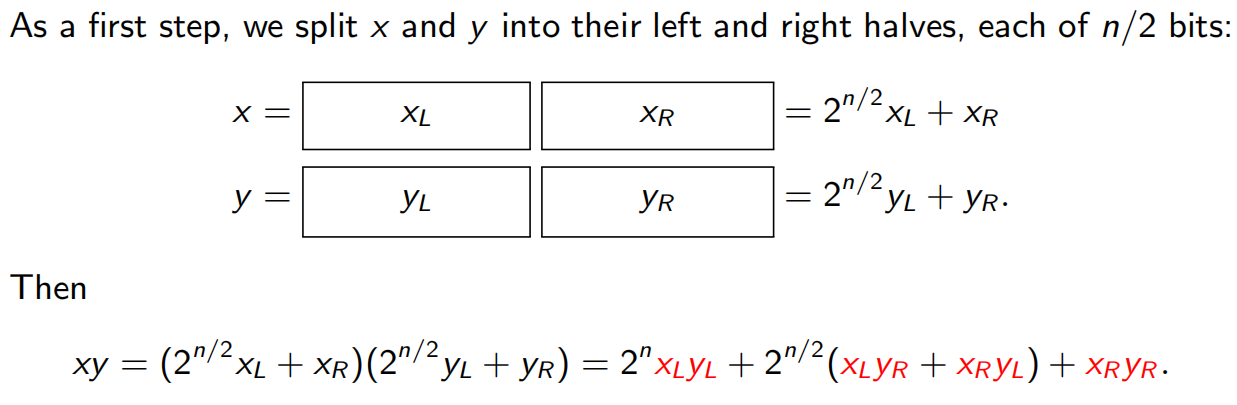
然后运用Gauss’ trick,把计算4个变成三个:

时间复杂度:
2.2 递推式
主定理:
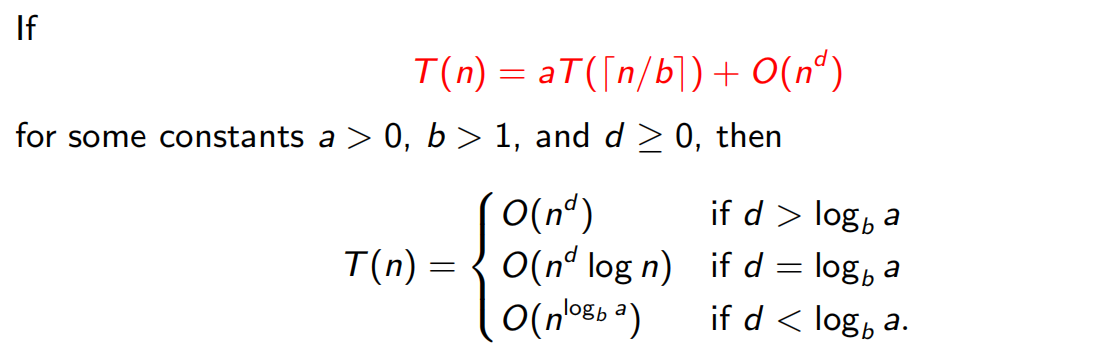
2.3 合并排序

时间复杂度:
对于仅使用比较的排序方法,有下界
2.4 寻找中项
寻找第 小的数:
用一个数 把 分成三部分 :比 小的,和 一样大的,比 大的。然后:
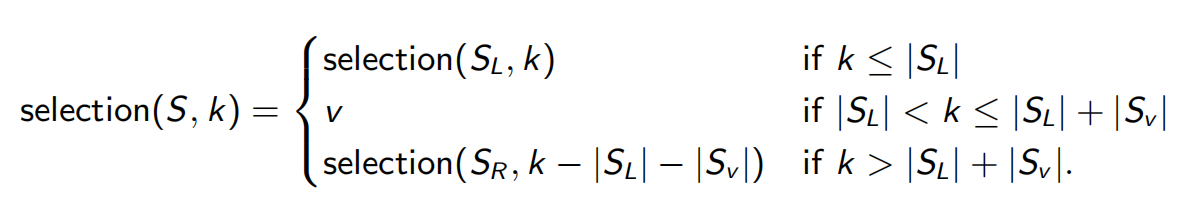
时间复杂度:最差 ,最好 , 平均?
由于是随机选取的 , 所以 在 25% ~75% 之间的概率是 50% ,而50%概率事件出现的期望次数为2次:
所以
2.5 矩阵乘法
8次变7次:
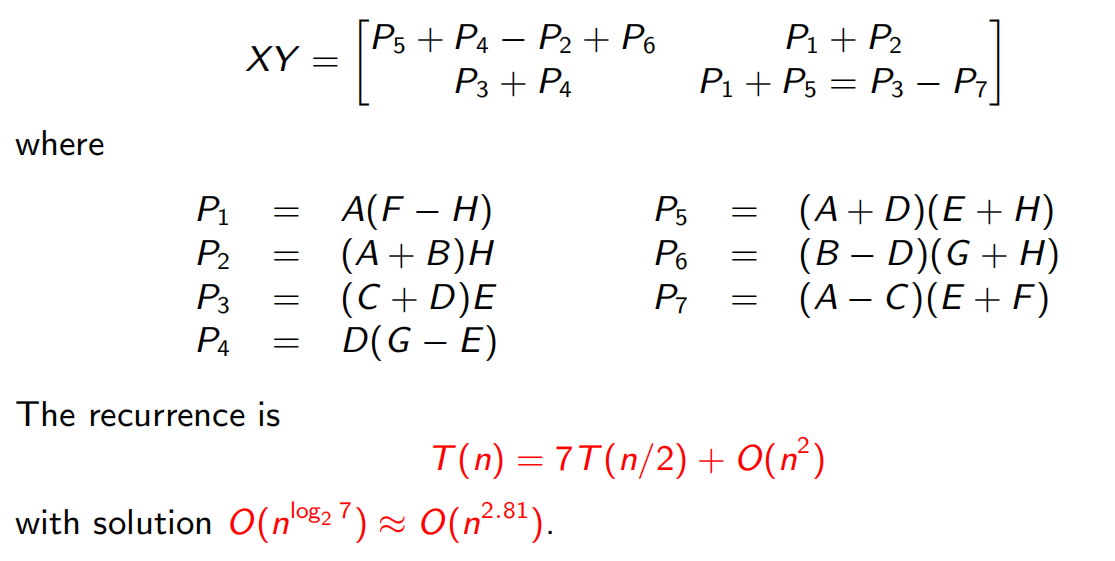
2.6 快速 Fourier 变换
2.6.1 多项式的另一种表示法
一个多项式 可以用两种方式表示:
- 系数表示:
- 值表示:
两种表示可以互相转换:系数表示计算得到值表示,值表示用插值得到系数表示。
计算多项式乘积的大致步骤:

2.6.2 计算步骤的分治实现
想法: 的系数表示 的值表示 的值表示 的系数表示
如果对于一般的 , 我们可能需要 的时间来计算这 个表达式的值,但是如果选取的比较好,我们就可以用 FFT 实现 的计算速度。
令

我们得到了:
2.6.3 插值
下面我们想要得到
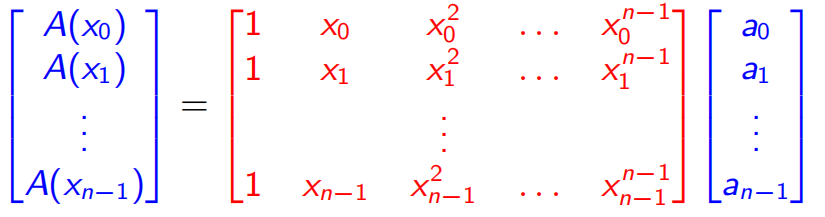
中间的矩阵 是一个范德蒙德矩阵,我们其实就是要求

于是我们只需要求 这样的矩阵了。
这可以使用一般的FFT来做,思想与多项式FFT类似:

2.6.4 快速 Fourier 变换的细节
第 3 章 图的分解
3.1 为什么是图
3.2 无向图的深度优先搜索
3.2.1 迷宫探索
3.2.2 深度优先搜索


EXPLORE 到的边是树边,其他的是回边。
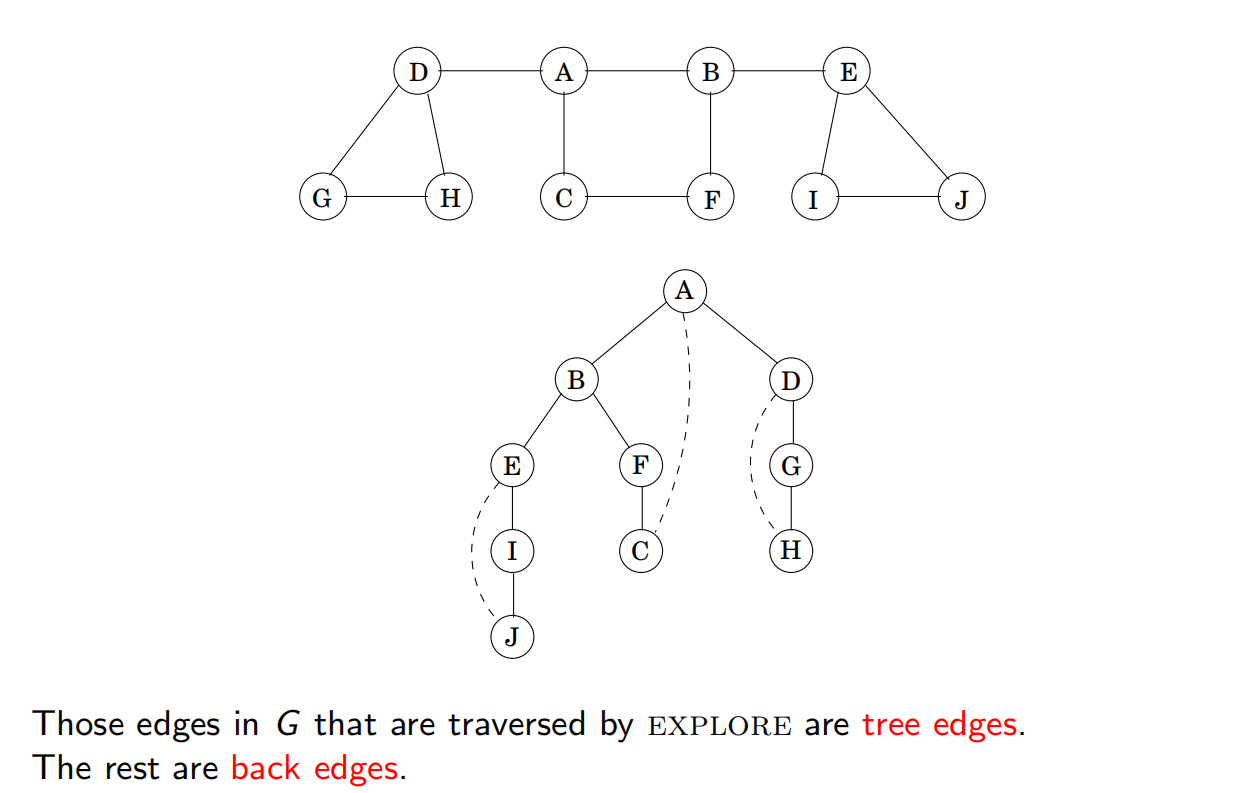
时间复杂度:
3.2.3 无向图的连通性
只需要把 设置为 , 在每次DFS中 EXPLORE 的时候++就可以获取所有的连通分量了。
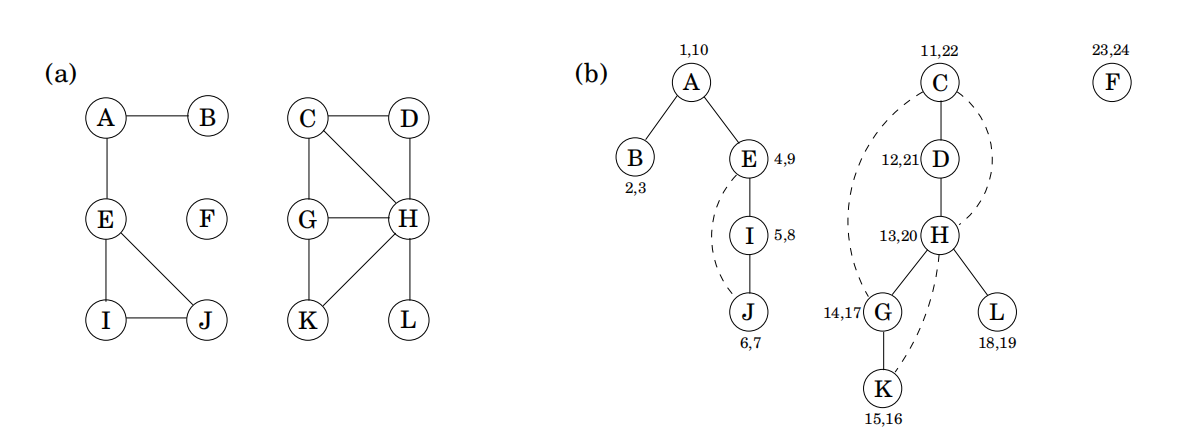
3.2.4 前序和后序
DFS序:


3.3 有向图的深度优先搜索
3.3.1 边的类型
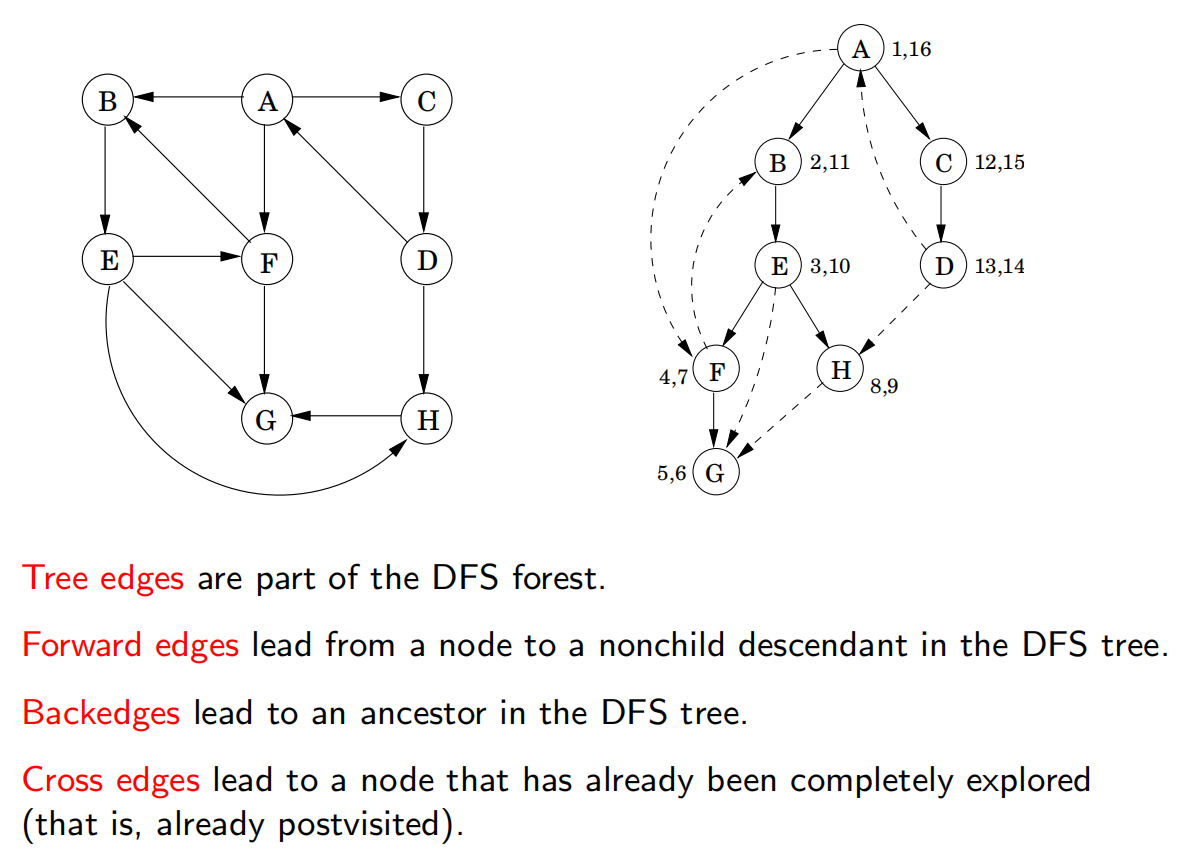

3.3.2 有向无环图(dag)
有回边 有环
线性化/拓扑排序:对所有点进行排序,使得所有边都从小点指向大点。
法一:由上图可以注意到, 顺序在没有回边的时候总是先 后 ,也就是说,每条边 都从 大的点指向 小的点,于是可以用 倒序排序作为一种线性化。
法二:dag一定有至少一个源点(source)和至少一个汇点(sink): 最小的点一定是源点,最大的一定是汇点
于是只需要每次找到一个源点并输出,删除,然后继续找就行了。
3.4 强连通部件
3.4.1 定义有向图的连通性
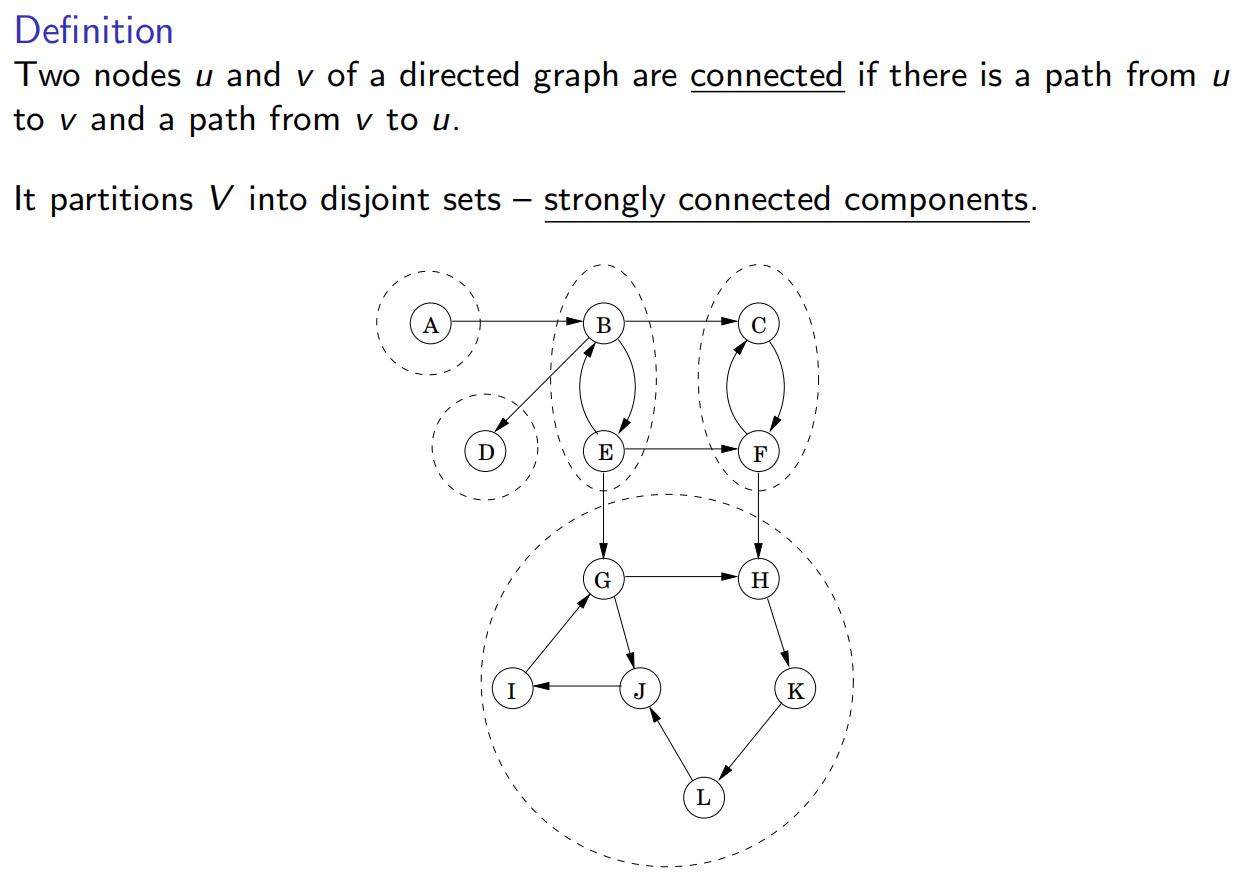
且每个有向图都是他的强连通分量的dag(有向无环图):
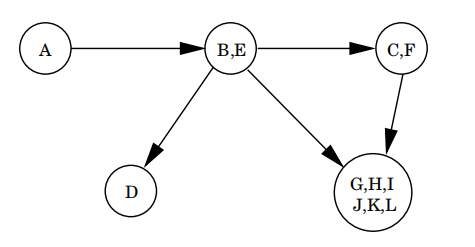
3.4.2 一个有效的算法
性质1 如果explore子过程从顶点u开始,那么该子过程恰好在从u可达的所有顶点都已访问之时终止。
因此,若我们对位于汇强连通分量(即在元图中表现为汇点的强连通分量)中的某个节点调用EXPLORE,就能获取该分量。
性质2 在深度优先搜索中得到的post值最大的顶点一定位于一个源点强连通部件中。
所以我们只需要把整个图反向, ,就可以在 中使用 DFS 得到 中post最大的,这个点在 的源点强连通部件中,也就一定在 的汇点强连通部件中。
性质3 如果 和 是强连通部件,同时从 中的一个顶点到 中的一个顶点存在一条边,则 中post的最大值要大于 中post的最大值。
于是我们得到一个最终算法:
理解: 中找post最大的,用这个点 EXPLORE 得到 的汇点连通分量,然后扔掉这个分量,找剩下的图中post最大的,再用 EXPLORE …
时间复杂度:线性
第 4 章 图中的路径
4.1 距离
4.2 广度优先搜索

queue:先进先出
对于每个 都曾经有一个时刻,满足以下条件:(1)所有与 之间的距离小于等于 的顶点被正确设定了距离;(2)其他顶点的距离都被设定为 ;(3)队列中只含有与 距离为 的顶点。

时间复杂度:
4.3 边的长度
4.4 Dijkstra 算法
4.4.1 广度优先搜索的一个改进
对于有权正整数边,直接变成若干个点
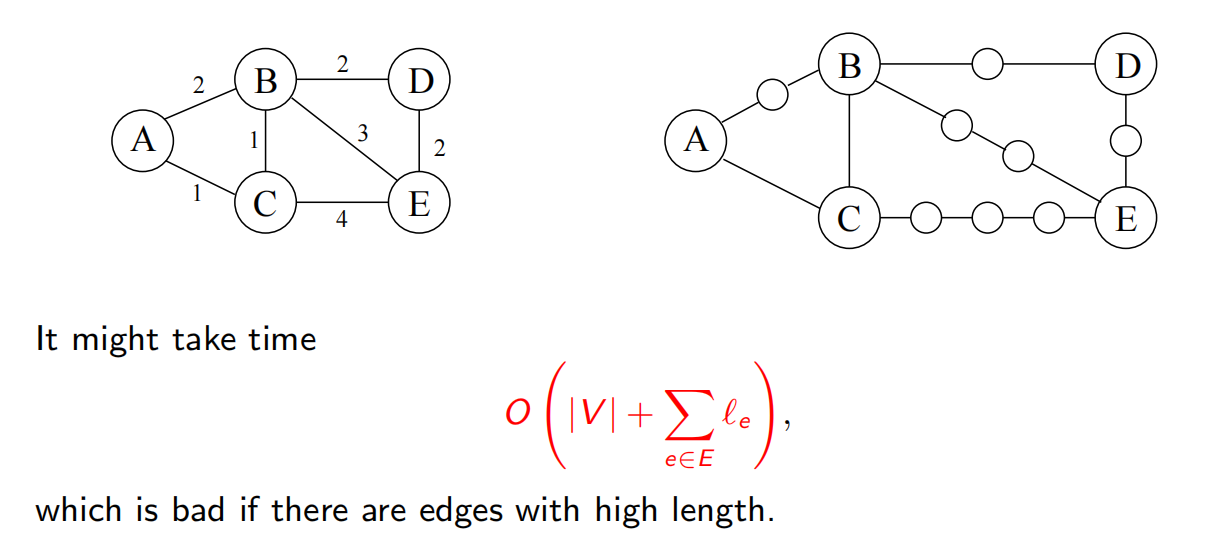
但是复杂度太高,需要改进——使用闹钟
形象的解释:用闹钟来记录:跳过中间的节点。

首先引入优先队列:
支持以下操作:
插入(Insert):向集合中添加一个新的元素。
减小键值(Decrease-key):用来减少某个特定元素的键值1。
删除最小元素(Delete-min):返回键值最小的元素,并且将它从集合中删除。
构造队列(Make-queue):用给定的元素以及给定的元素键值构建一个队列。
然后使用优先队列来严谨书写Dijkstra算法:

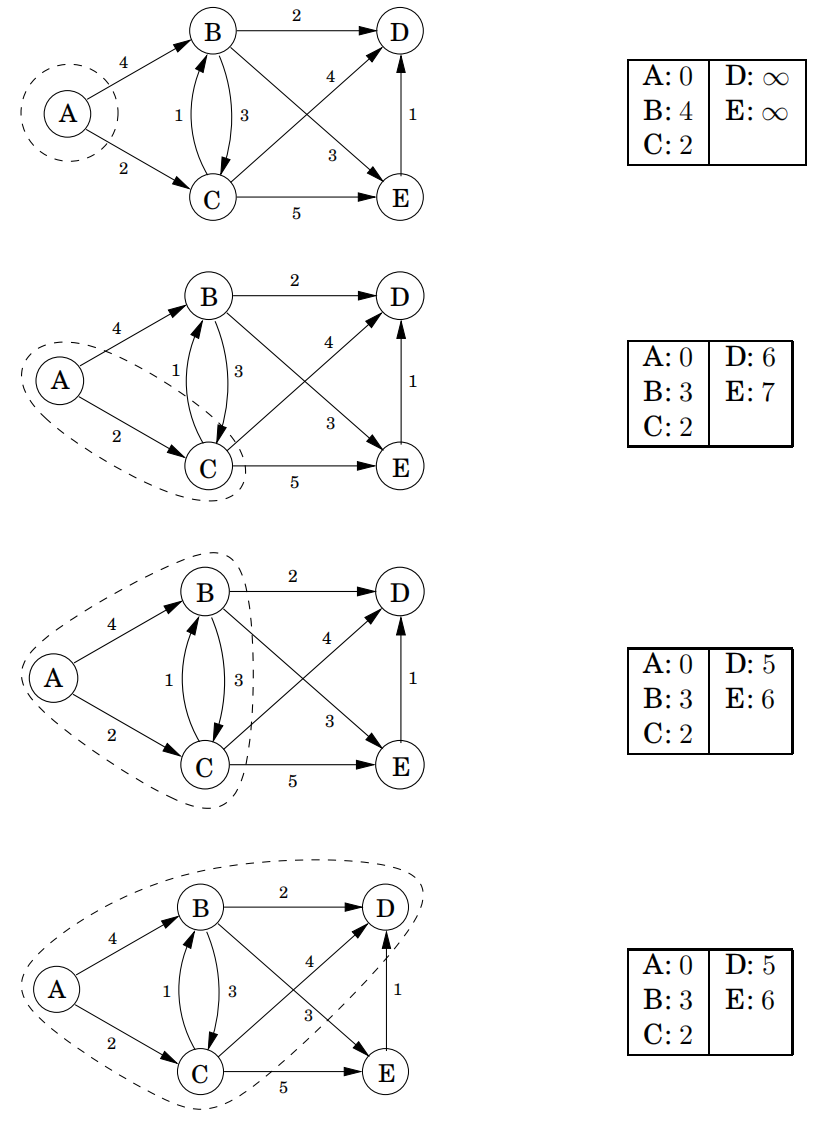
4.4.2 另一种解释
在每次 while 循环迭代的末尾,有以下条件成立:(1)存在一个值 ,使得从 到 中所有顶点的距离小于等于 ,同时使得从 到 外所有顶点的距离大于等于 ;(2)对于每个顶点 , 表示一条从 到 的最短路径的长度,该路径经过的顶点均在 中(如果不存在这样的路径, 值设为 )。

4.4.3 运行时间
总共需要 次 deletemin 操作和 次 insert/decreasekey 操作
取决于使用的优先队列实现方式,eg.二分堆实现,时间复杂度:
4.5 优先队列的实现
列表:

4.5.1 数组
4.5.2 二分堆
元素被存储在一个完全二叉树中,即二叉树每层上的节点都被从左到右地填满,并且在上一层未填满之前不会出现下一层。另外,需要遵循一种特殊的顺序:树中任意节点的键值必须小于等于其后裔节点的键值。因此,特别的,根节点一定对应着键值最小的元素。
插入(Insert):先插入到尾部,然后不断和父亲交换(称为冒泡)
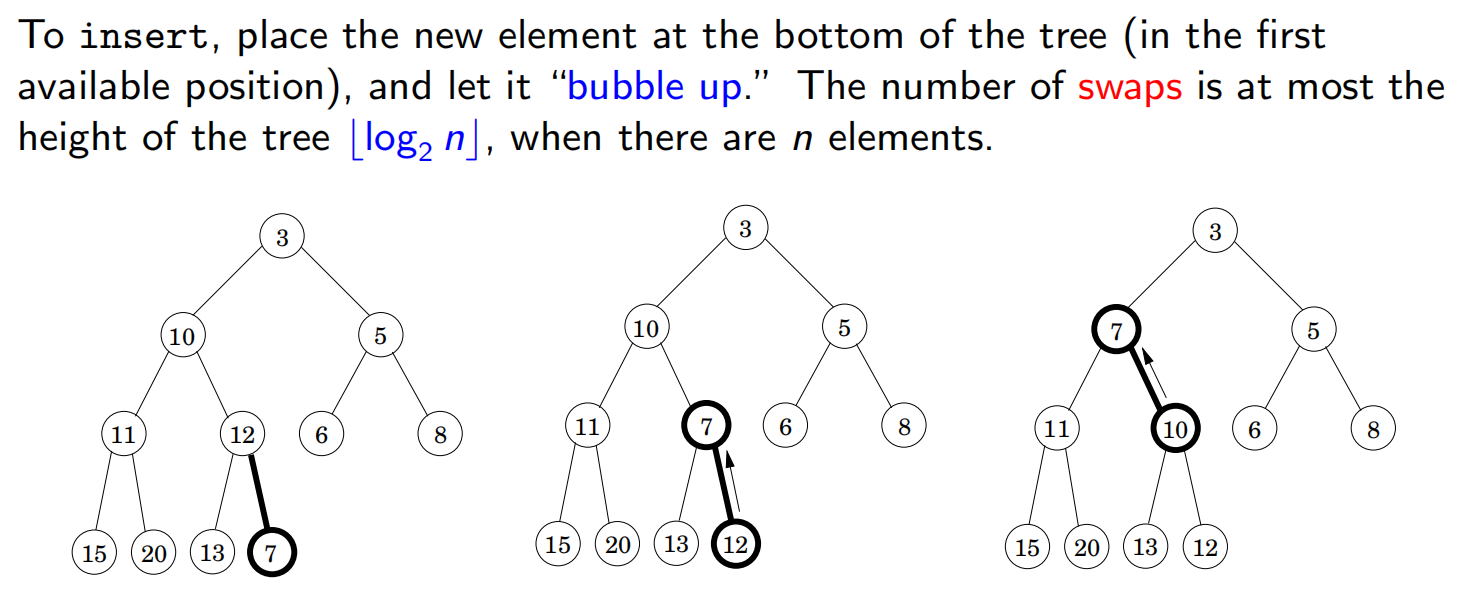
减少键值(decreakey)和插入类似。
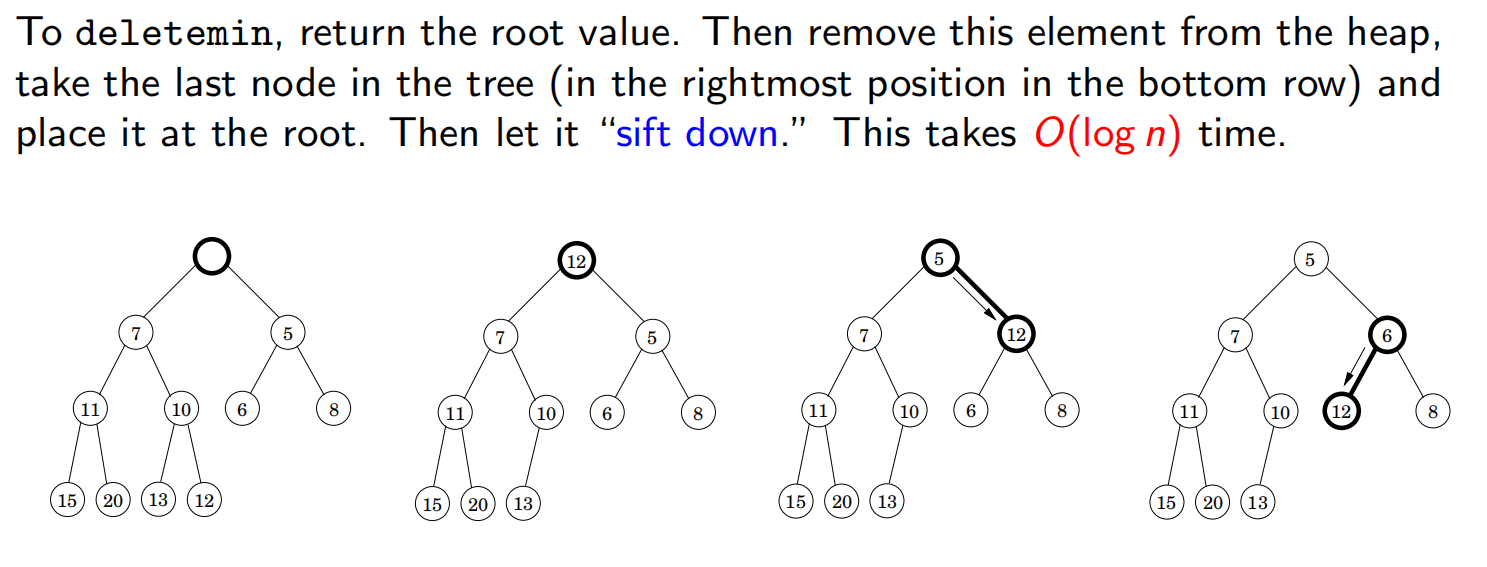
删除最小元素(deletemin):删除根,用尾部元素代替这个根,然后再不断地和所有孩子比较并交换。时间复杂度:
4.5.3 d 堆
每个节点有 d 个儿子。树的高度缩减为
插入操作时间复杂度为
删除最小元素时间复杂度为
4.6 含有负边的图的最短路径
4.6.1 负边
在有负边的时候,Dijkstra算法失效。但是值得注意的是,在Dijkstra算法中,dist永远大于等于最优的dist,也就是说,在每次update的时候,dist永远是safe的。所以我们只要在每次update的时候update所有的边(比较暴力),就可以得到Bellman-Ford算法:

时间复杂度:
4.6.2 负环
通过Bellman-Ford我们还可以轻松地检测负环:
我们只需要在 次迭代之后再多执行一次迭代过程。图中存在一个负环当且仅当在这最后一次迭代中有某个dist的值被减少。
4.7 有向无环图中的最短路
有两类图直接排除了负环存在的可能性:一类是不含负边的图,另一类是没有环的图。前一种直接用Dijkstra即可,后一种,即有向无环图(dag)中,我们下面给出线性时间的算法。注意到:
在dag的任意路径中,顶点是按照图线性化产生的顶点序列的升序排列的。
因此,进行以下步骤足矣:通过深度优先搜索线性化(即拓扑排序)有向无环图,然后按照得到的顶点顺序访问顶点,对从当前访问顶点出发的边执行更新操作。

第 5 章 贪心算法
5.1 最小生成树
5.1.1 一个贪心方法
形式化:
Kruskal算法:不断重复地选择未被选中的边中权重最轻且不会形成环的一条。

5.1.2 分割性质
Kruskal算法的正确性由分割性质(Cut property)保证。

证明:
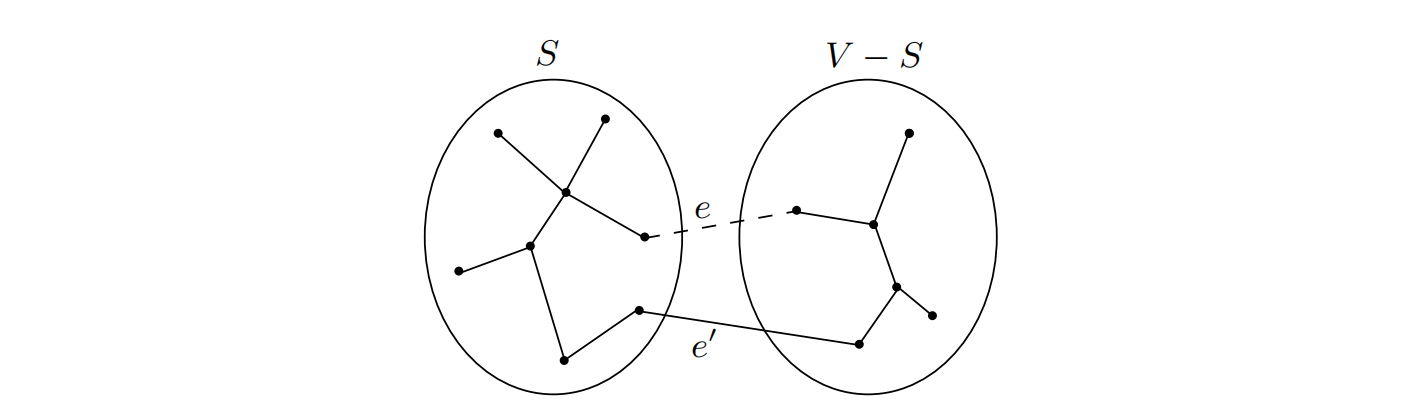
T是MST,若不包含 ,由于连通,一定包含 ,则把 换成 之后得到的 边权小于等于 。所以一定等于 也是MST。
5.1.3 Kruskal 算法

5.1.4 一种用于分离集的数据结构
表示 的父亲, 表示其下悬挂的子树的高度。
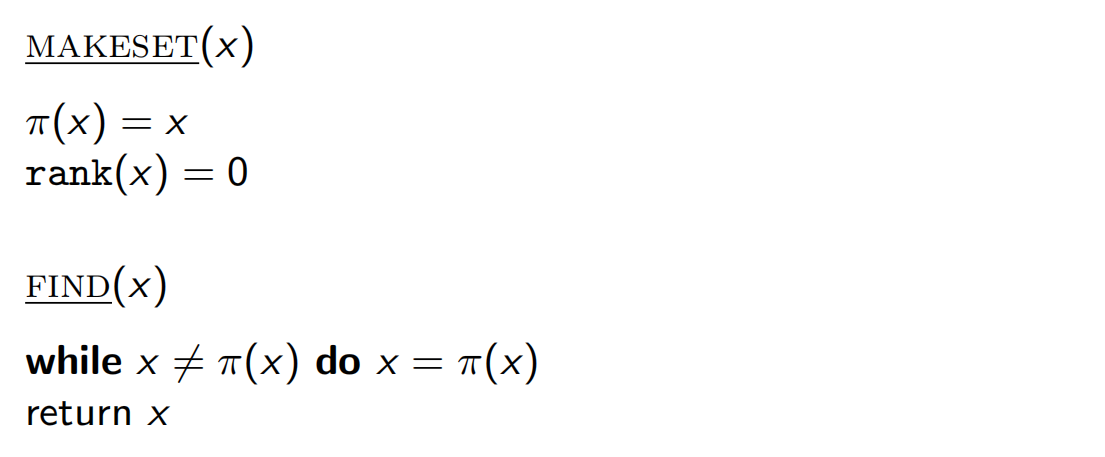

一些性质:


改进并查集:
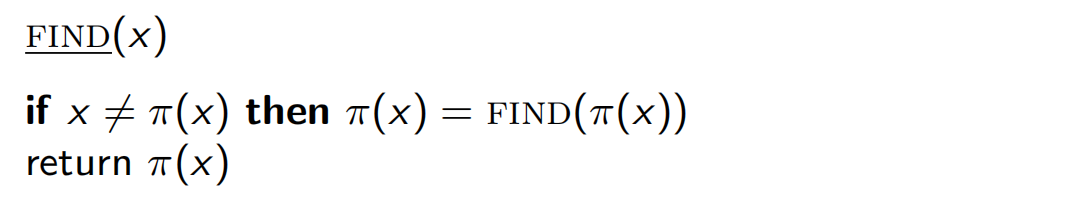
均摊复杂度降至
复杂度证明:先证明性质1~3仍然成立,然后用“零花钱”来说明。具体见书上P152~P153,为了避免笔记过长,这里仅把链接贴在这里。
5.1.5 Prim 算法
(Kruskal算法的变体)

笔者注:很多同学可能对于MST和SPT(最短路径树)比较混淆,对于Dijkstra以及Prim也比较混。这里做简单的区分:MST求的是整体的最小性质,估计全局,SPT只是一个固定源点s到每个点的最短路,二者关注的内容是不一样的。考虑一个简单的例子:
1 | A |
在Dijkstra以A为源点的时候,得到的SPT是A-B,A-C,而MST是有B-C的,这就是因为A在找最短路的时候不会考虑整体
5.2 Huffman 编码
5.3 Horn 公式
5.4 集合覆盖
Set Cover问题:


虽然这个贪心不是最优的,但是不会太差:

证明:设 为贪心算法中经过 次迭代后仍未覆盖的元素数量()。由于这些剩余的元素能被最优的 个集合覆盖,因此,当前一定存在某个包含其中 个元素的集合,贪心至少会选取 个元素。
第 6 章 动态规划
6.1 重新审视有向无环图的最短路径问题
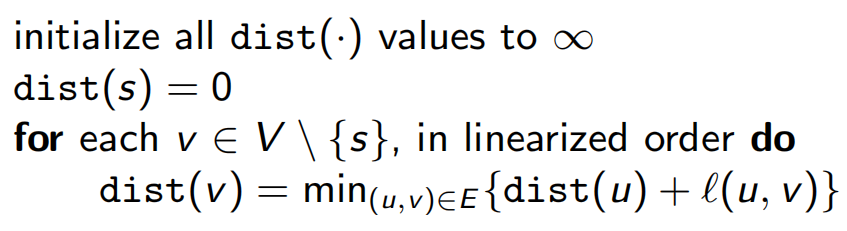
6.2 最长递增子序列


6.3 编辑距离
找两个字符串之间的最大匹配度。


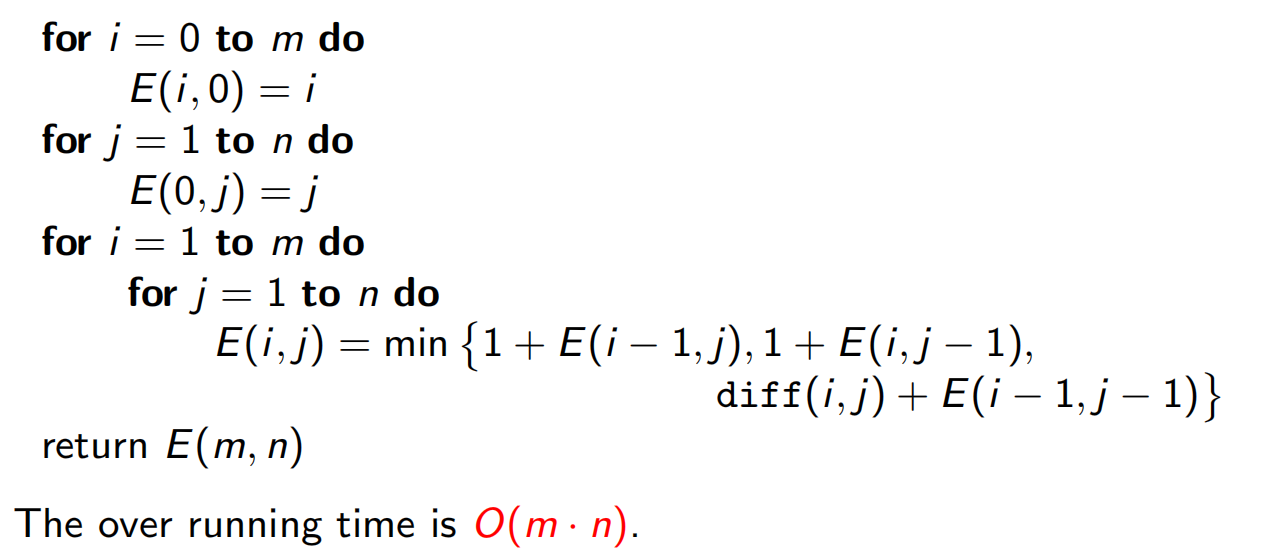
6.4 背包问题
可重背包:每种物品可以选很多次。

无重背包:

6.5 矩阵链式相乘

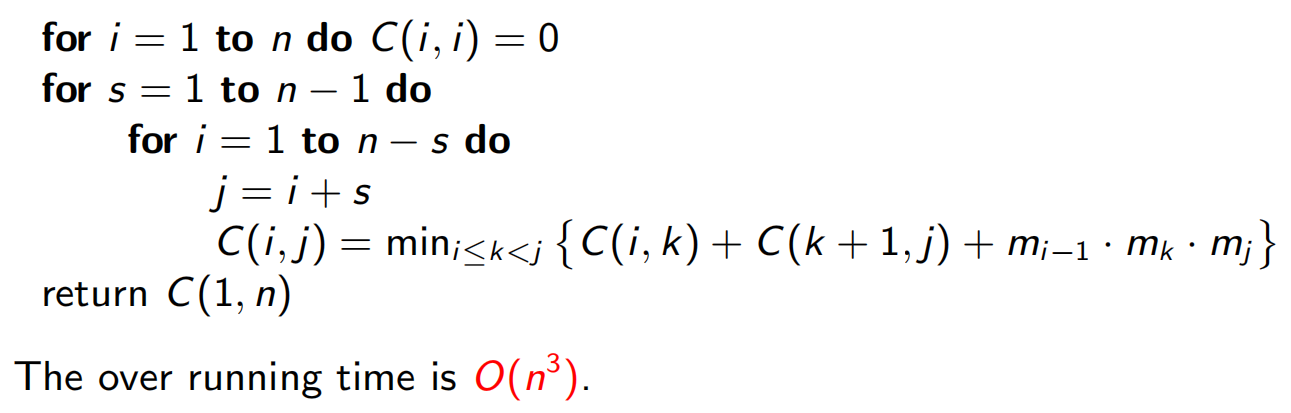
6.6 最短路径问题(TSP)


6.7 树中的独立集

第 7 章 线性规划与归约
7.1 线性规划简介
给定一组变量,并希望为这些变量分配实数值,以便: (1) 满足一组涉及这些变量的线性方程和/或线性不等式; (2) 最大化或最小化给定的线性目标函数。
单纯形法:
算法从一个顶点开始,例如在我们的例子中可能是(0,0),不断重复地寻找利润(目标函数)值较高的邻居顶点(该顶点与原顶点由可行区域的一条边相连),并向其移动。通过一种历经多边形顶点的爬山方法,从一个邻居到下一个邻居,算法将沿路不断提高利润。一旦再也找不到利润更高的邻居,单纯形法将得出结论,宣布当前顶点为最优解,同时结束计算。
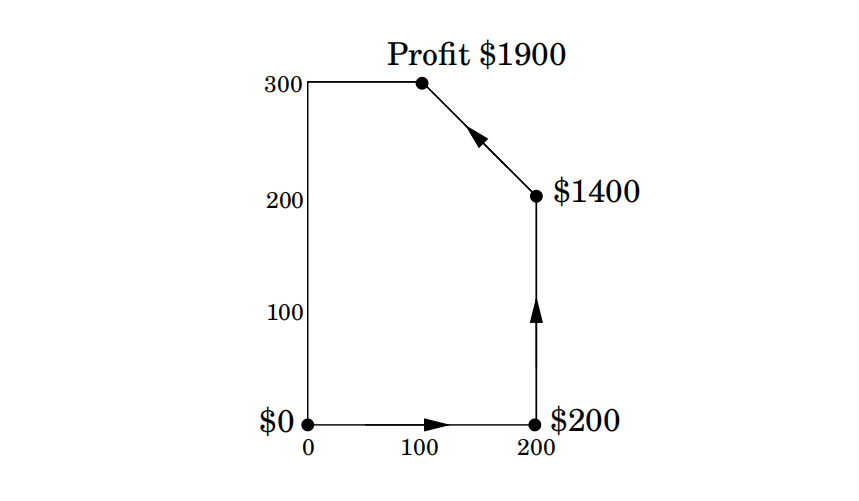
正确性:回想一下我们之前分析指出的利润线的移动特征。由于最终相交顶点的所有邻居都位于该直线之下,因此可行多边形中的剩余部分也必然都位于该直线的下方(请注意可行区域是一个凸多边形!)。
归约:
我们想要解决问题P。我们已经拥有一个能解决问题Q的算法。如果任何用于Q的子程序也能被用来解决P,我们就说P可归约至Q。
通常,P可以通过对Q子程序的一次调用来解决,这意味着P的任何实例x都能被转化为Q的实例y,从而使得P(x)可以从Q(y)推导得出。
线性规划的变体:
一个普通的线性规划形式上往往具有很大的自由度:
1.它可能是最大化问题也可能是最小化问题;
2.约束条件可能是等式也有可能是不等式;
3.变量通常非负,但事实上它们也可以具有任意符号。
但可以通过归约相互转换:

这样就可以归约为标准形式:
所有变量均为非负数,所有约束条件均为等式,且目标函数需最小化。
7.2 网络流
7.2.1 石油运输
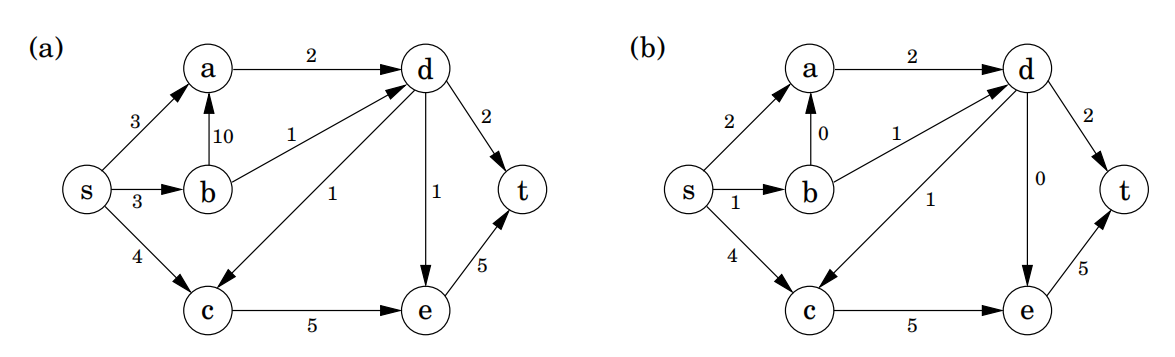
7.2.2 最大流
描述:在不超过每条边容量的前提下,我们希望由 向 输送尽可能多的石油。
书上的描述 以及 Slides中的描述
这样就转化为了线性规划问题,可以用单纯形法解决。
7.2.3 对算法的深入观察
在每次迭代中,单纯形法寻找 到 的一条路径,其中的任意边 可能为如下两种类型之一:
1. 包含在最初的网络中,并且未达到最大流量;
2.其反向边 在最初的网络中,并且其中已存在一定的流量。
如果当前的流为 ,则对于第一种情况,边 最多还能接受 的多余流量;而在第二种情况下,最多增加的流量为 (取消 上的全部或部分流量)。这类增加流量的机会可以由剩余网络 来判定,该网络包含了所有的以上两类边,并标出了其剩余流量 :
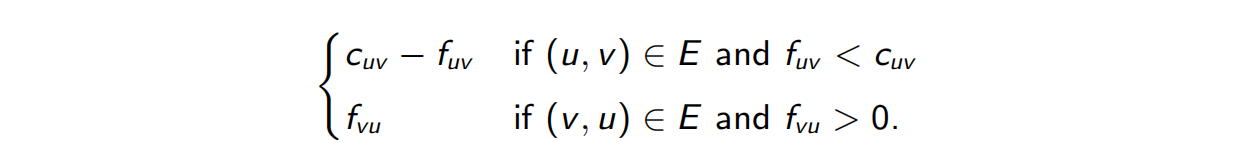
该算法采取迭代的方式进行,每次先构造一个 ,然后利用线性时间的广度优先搜索在 中寻找 到 的一条可行的(能够继续提高流量的)路径,找不到任何这样的路径时算法停止。
7.2.4 最优性的保证
将节点分为两部分 和 :
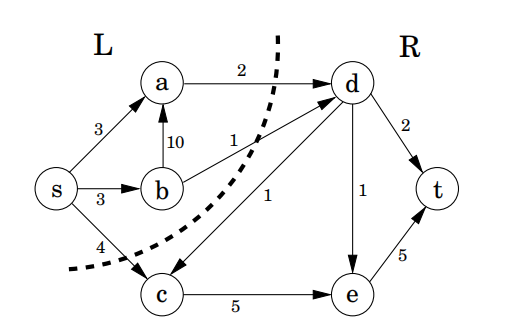
这三条边作为一个割,,任意一次石油传输都必须经过L到达R。因此,没有哪个流的规模能够超过L到R的边的总容量,所以最优。一般地,对于任意流 和任意 分割 。 。事实上,我们有:
最小分割最大流定理 网络中最大流的规模等于其中 分割的最小容量。
进一步,最小割可以在我们的算法中作为副产品得到。
为算法终止时得到的流,记 为 中可由 出发到达的所有节点集合, 。我们断言:
为了证明其正确性,由 的定义,不难发现任意由 到 的边必然都是“满”的(当前流 使用了其全部流量),而任意由 到 的边流量都为0。也即 且 。由此可知,跨越 的流量应该就等于该分割的容量。
7.2.5 算法的效率
每次迭代 ,假设在最初的网络中所有边的容量都是一个不大于 的整数,注意到最大流量最多为 ,迭代的次数应该也最多为 。如果不能选择恰当的路径,最终的迭代次数将与 成正比。但采用广度优先搜索将使得找到的路径包含最少的边,则不论边的容量如何,最终的迭代次数将不超过 。而该上界保证了对最大流来说算法总的运行时间为
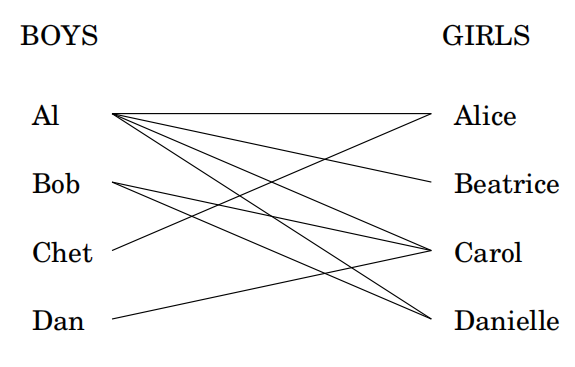
7.3 二部图的匹配
左侧四个节点代表男孩,右侧四个节点代表女孩。是否可能配对所有的男孩女孩,并且配对双方连边?在图论中,这样的配对称为一个完美匹配。
以上的配对游戏可以被归约到最大流问题,因此它也是一个线性规划问题。定义一个拥有流向所有男孩的边的源节点 ;一个拥有从所有女孩流出的边的汇节点 ;同时对应于原图中的所有边在新图中加入由男孩流向女孩的边。最后,赋予所有的边容量1。
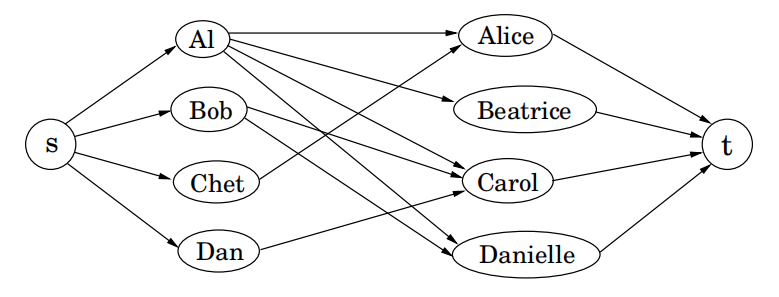
性质:如果所有边的容量为整数,则由我们的算法得到的最大流的规模也为整数。
7.4 对偶
要解决
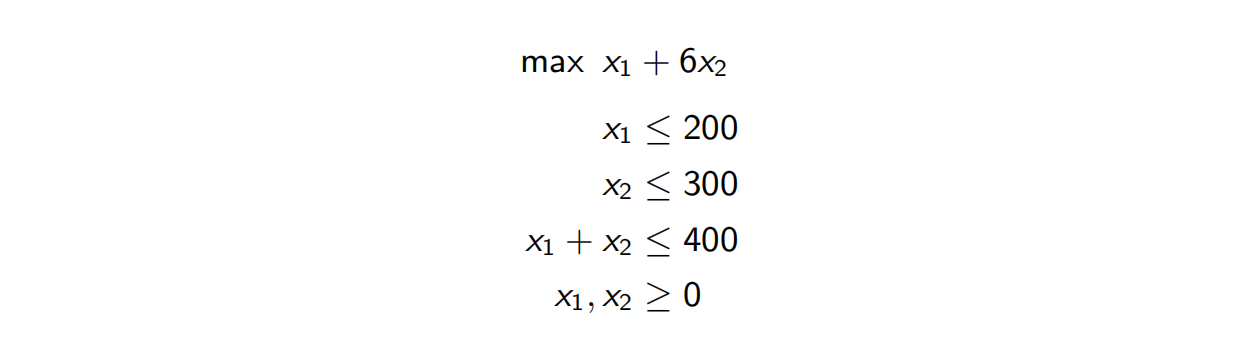
等价于
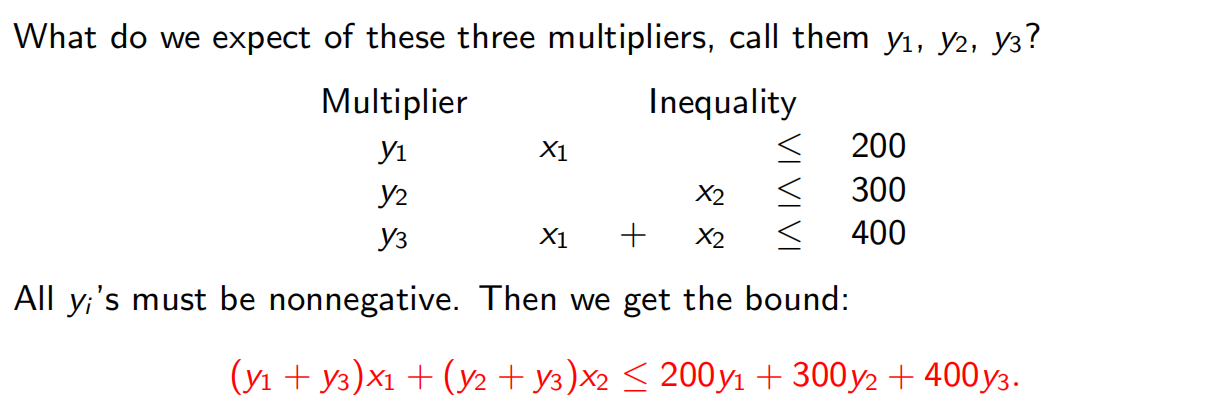
所以我们实际上是在求
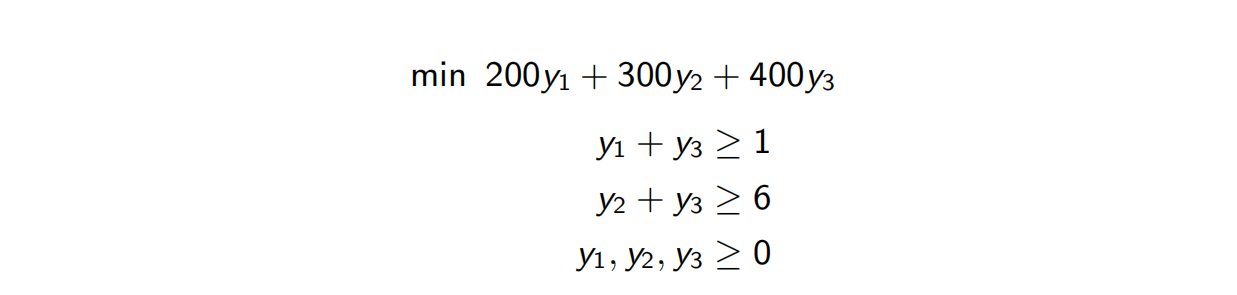
。而实际上,这两个问题的最优值都是1900,从而对于各自的LP都是最优的。
事实上,每个LP问题都有一个对偶问题。
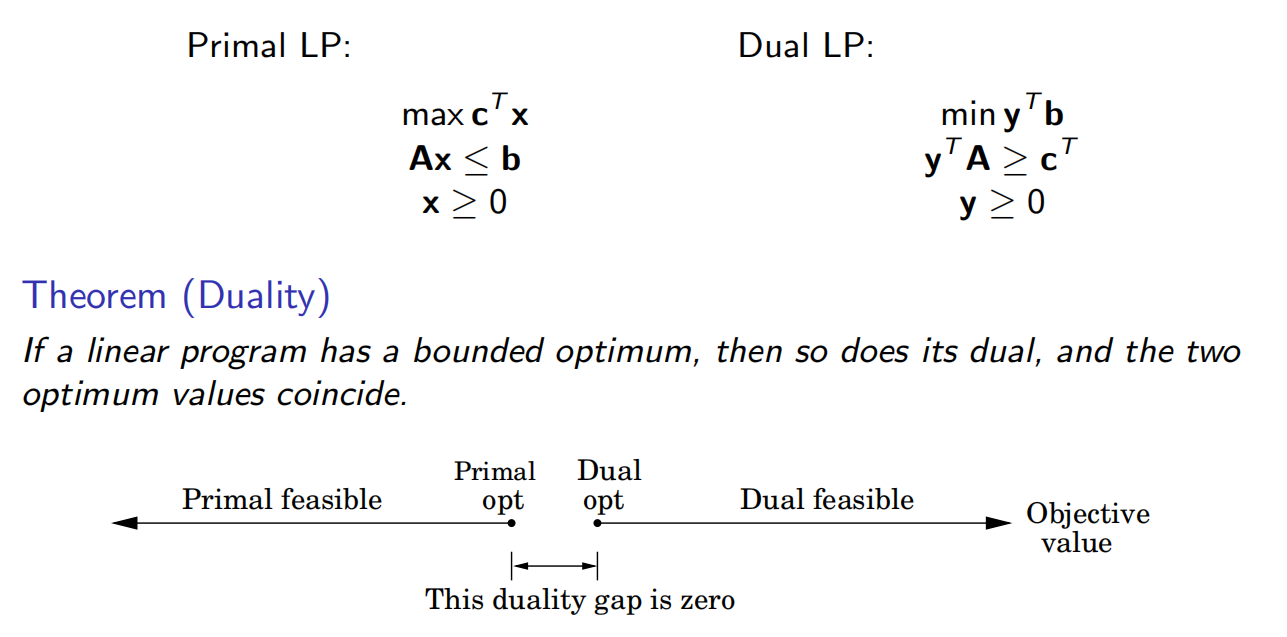
7.5 零和博弈(游戏)
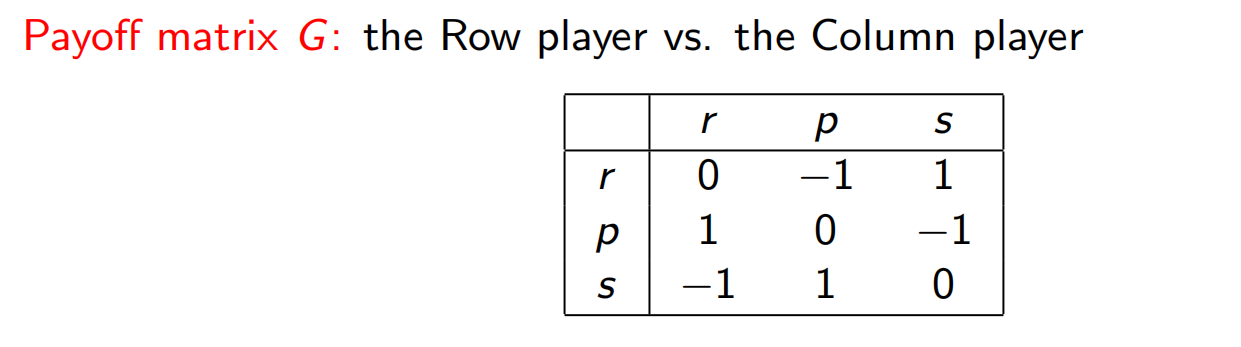
重复以上游戏。在每一回合中Row以 的概率选择 r、以 的概率选择 p、以 的概率选择 s。该策略用向量形式表示为 ,其中的分量值均非负且总和为1。类似地,将Column的混合策略记为 。

假设Row采用一种“完全随机”的策略 。则无论column怎么做,期望都是0.所以,Row最坏最坏打成平手。对手亦然。
现在换一种稍微不同的方式,考虑以下两种场景:
1.首先由Row宣布自己的策略,然后Column再选定策略;
2.首先由Column宣布自己的策略,然后Row再选定策略。
我们已知知道了如果玩家都采取最优的策略,则对于任何一种情况,平均支付都相同,为0。这一重要的性质事实上源自线性规划的对偶性——或者说,该性质与对偶性是等价的。
让我们通过一个非对称的博弈对其进行研究。考虑一个总统选举的场景。其中有两名候选人,他们的行动表现为选择不同的核心议题(比如经济(e)、社会(s)、道德(m)和减税(t)纲领。支付矩阵G中的每个位置对应于Column(在此他和Row一起变成了总统候选人)丢失的选票数。
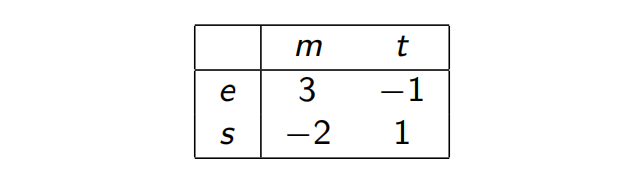
所以Row要做的是

等价于
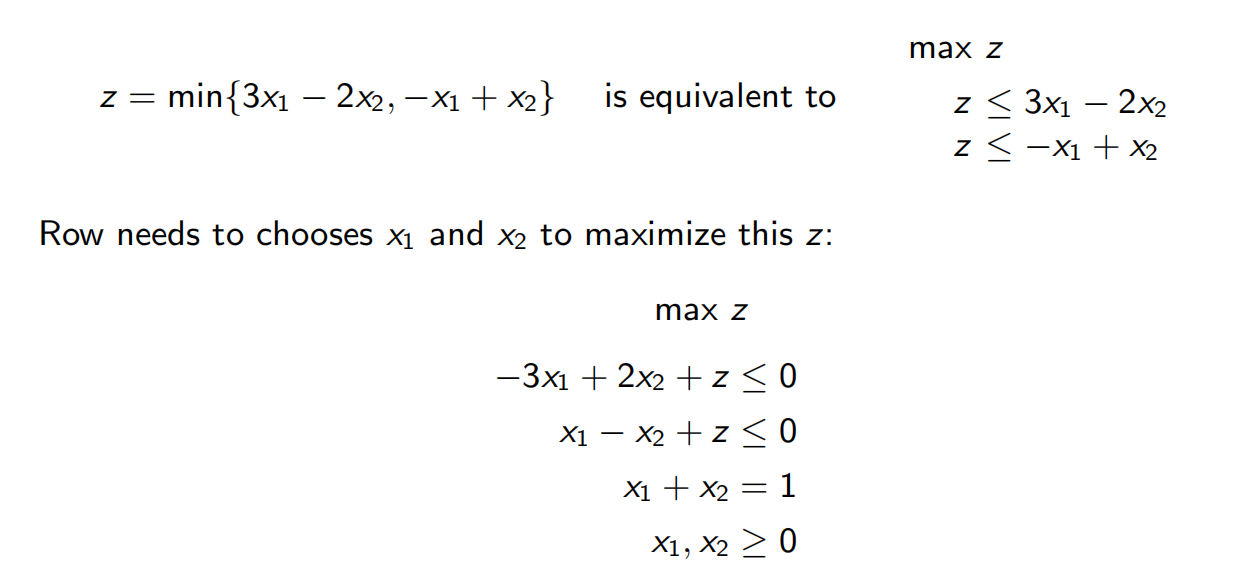
同理Column:
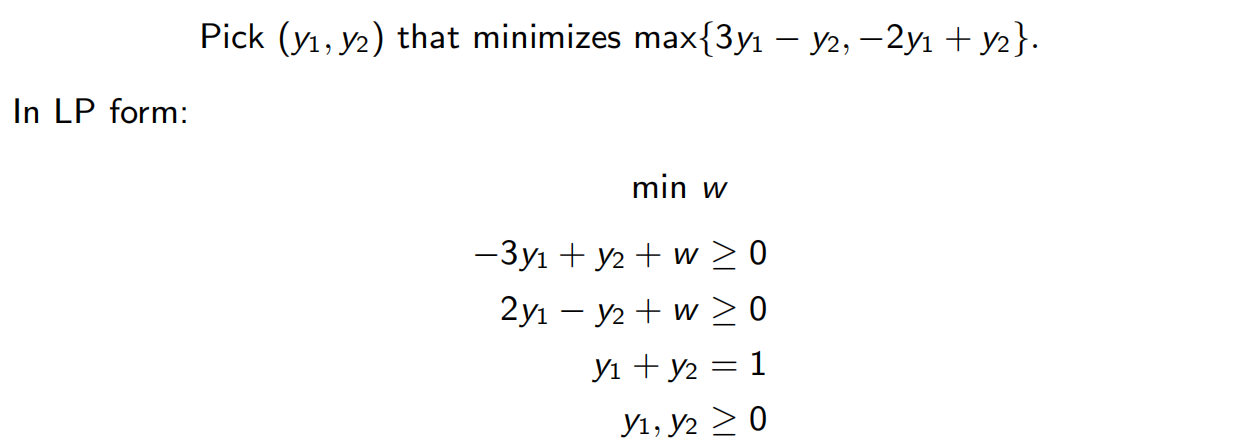
二者对偶,有相同的最优值V
总结:通过求解一个LP,Row(追求最大化者)能够在无视 Column 策略的情况下,确保至少V的支付。而通过求解对偶LP,Column(追求最小化者)也能够在无视Row 策略的情况下确保最多V的支付。接下来还可以发现,对于二人这都是唯一可行的最优策略—即使在我们事先无法确定游戏中宣布策略先后的情况下,双方也应该优先选择该策略。在此,V称为该游戏的价值。
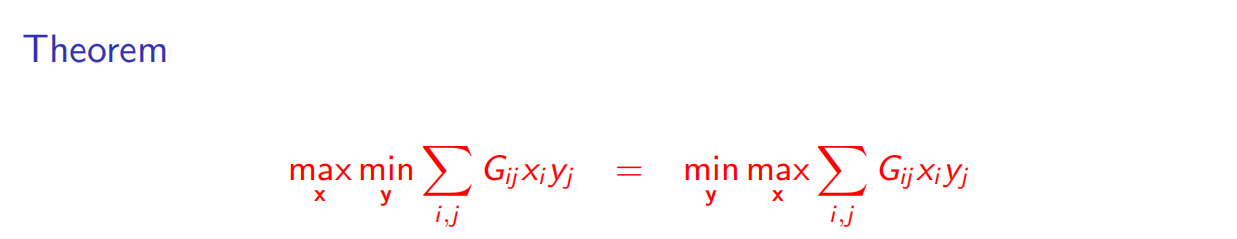
这看起来有些令人意想不到,因为等式左侧对应于Row先宣布策略的场景,我们曾经推测会产生有利于Column的结果,而右侧对应的Column先宣布策略的场景也曾被认为是对Row有利的。现在我们看到,正如对偶性对最大流和最小分割所做的那样,它使得两种不同情形的结果变得完全相同了。
7.6 单纯形算法
7.6.1 n 维空间中的顶点和邻居
选择约束不等式的一个子集。如果存在唯一的点满足其对应的所有等式,且该点恰好也是可行的,则其为一个顶点。当存在n个变量的时候,需要n个线性方程。所以,每个顶点都是由n个不等式所定义的。若两个顶点对应的所有不等式中有n-1个相同,则它们互为邻居。
7.6.2 算法
在每次迭代中,单纯形法需要完成如下两项任务:
1.检查当前顶点是否最优(如果是,则退出)。
2.决定向哪里移动。
首先对于原点讨论。对任务一,原点最优当且仅当所有的 。(需要b > 0)
对任务二,我们可以通过增大对应于 的 来进行移动。也即,我们放松已经“绷紧”的约束 ,让 增大,直到某个原来“松弛”的约束被“绷紧”。在该点上,我们再次得到了恰好n个紧的不等式,故我们到达的是一个新的顶点。
对于一般的顶点u呢?我们把他归纳到原点(坐标变换):我们看u的局部视图,这类重新定义的局部坐标包含了其中的点到n个超平面的距离(经过适当放缩后) ,而这n个超平面定义和包围了u:
特别地,如果包围u的一堵“墙”(超平面)对应的不等式为 ,则由一个点x到这堵“墙”的距离为
把x坐标变成y坐标,“修改”后的 LP具有如下三点性质:
7.6.3 补遗
起始顶点:

对于这个新的LP,容易找到一个起始顶点,即对所有i满足 ;且其它变量都为0的点。因此我们可以用单纯形法求得其最优解。
存在两种情况。如果 的最优值为0,则由单纯形法求得的所有 都为0。由新LP的这一最优顶点可知,我们只需忽略所有的 ,即可得到原LP的一个可行的起始顶点。然后我们就可以开始运行单纯形法了。如果以上的最优值是正的,说明原来的线性规划不可行。
退化:
一般的顶点用n个式子框定。但是有些点用了多于n个,称为退化。
比如,在我们想要max -x+z的时候。一开始在原点,原点是退化的,由1、3、4、5框定。但一开始只由3、4、5式子产生。任意松弛一个式子都无法到达opt点:1、2、3式子产生。但是如下图,这个点确实是原点的邻居。所以我们可能需要把3、4、5变成1、3、4.要不然,一开始想松弛5的时候由于 ,z就死在这儿了。但结果却可能事与愿违,导致单纯性法最终陷入无限循环。
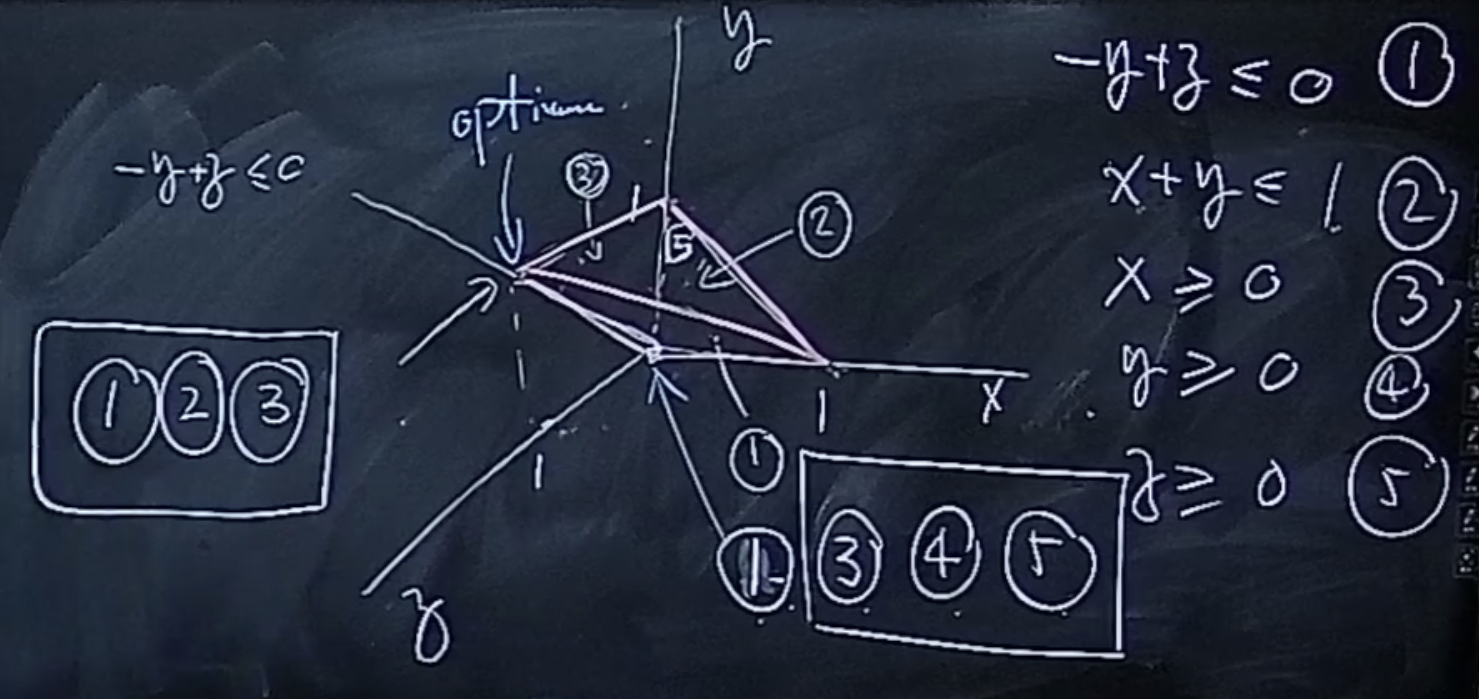
修正:把方程右边的b改一点。这样就不会有退化的点了。

无界性:
有些情况下LP是无界的,此时目标函数能够取任意大的值。如果存在这样的情况,在探索某个顶点的邻居时,单纯形法会注意到移除一个不等式并加入一个新的不等式后,新的线性方程组将没有确定的解(也即其有无穷多的解)。并且事实上(这是一个简单的测试)其解空间包含了一整条直线,沿着该直线能够使得目标函数值变得越来越大,直到∞。此时单纯形法将会退出并报告该情况。
7.6.4 单纯形法的运行时间
由于每次迭代只有一个不等式被替代,我们实际上可以在 下重写LP,

如此一来,每次迭代就只需要 。至多 次迭代(顶点上限)。所以单纯形法实际上是指数级别的。
7.7 后记:电路值(Circuit Value)
布尔电路:一个由以下几类门电路(简称门)构成的有向无环图(dag):
- 输入门(input gate):入度为0,值为 true或 false。
- 与门(AND gate):入度为2。
- 非门(NOT gate):入度为1。
此外,某一个门被指定为输出。
所谓电路值问题:如果将布尔逻辑按照门的拓扑顺序加以应用,输出是否为 true?
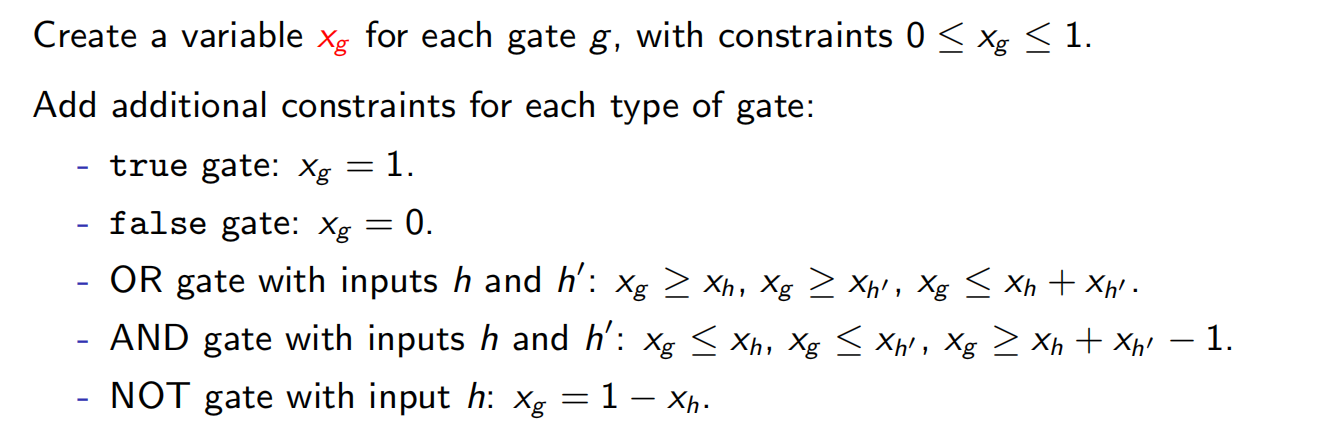
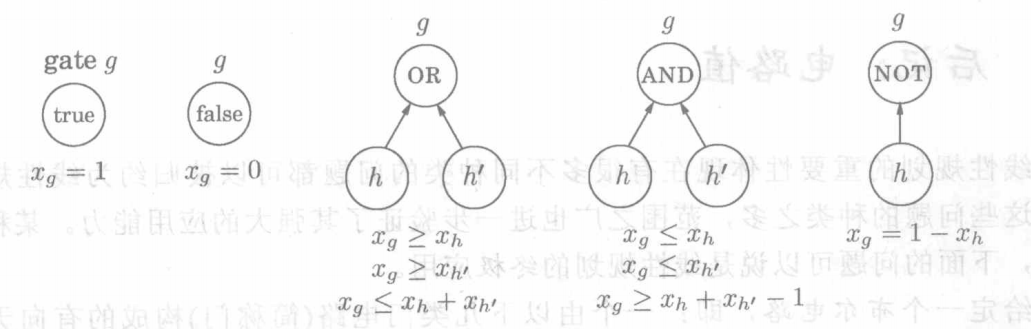
这些约束要求所有的门都必须取正确的值—0代表 false,1代表 true。我们不必求最大值或最小值,而只需从对应于输出门的变量x。中读取结果。
变成一个LP问题
第 8 章 NP - 完全问题
8.1 搜索问题
SAT问题(可满足性问题)

CNF:合取范式。SAT问题即为:给定一个采取合取范式的布尔公式,为其找到一个可满足赋值或判定该赋值不存在。
SAT是一个典型的搜索问题。给定一个问题实例 ,我们需要求它的一个解 (即某个符合特定描述的对象。在我们当前的问题中为一组满足所有子句的赋值)。如果这样的解不存在,则称该问题不可解。
一个搜索问题必须具有如下性质:对实例 ,其任意一个解 的正确性都应该能被快速地检验。能被快速检验意味着存在一个以 和 为输入的多项式时间算法,用于验证 是否为 的一个解。
搜索问题的完整定义:

TSP问题(旅行商问题)
我们需要确定一条旅行路线,该路线为一个恰好经过每个顶点一次的环,且总的旅行费用不能超过 b
可以看出这是一个搜索问题(存在算法C,直接把所有路径加起来看是否小于b)
这里我们叙述的是:是否有不超过b的(搜索问题),而不是最优化问题。但其实二者是等价(难度一致)的。(搜索通过二分答案可以解决最优化问题,最优化问题也可以直接解决搜索问题)
Euler 和 Rudrata
Euler:七桥问题
定义一个称为 Euler 路径的搜索问题如下:给定一个图,寻找一条恰好包含每条边一次的路径。从 Euler给出的答案出发,稍加思考不难发现,这一搜索问题能在多项式时间内求解。
Rudrata:象能否从某个棋盘格出发,不重复地走遍所有的棋盘格,并最终回到出发的格子
定义Rudrata环路搜索问题如下:给定一个图,求一条经过每个顶点恰好一次的环路,或者,报告该环路不存在。
Minimum Cut and Balanced Cut(分割与二等分)
分割是一个边的集合,将其从图中移除将导致图不再连通。
最小分割问题:给定一个图和预算b,求最多包含b条边的分割。(可以用最大流最小割,每条边设置容量为1,在多项式时间内通过计算n-1次最大流而求解。具体来说,令每条边容量为1,然后求某个确定节点到其它每个节点的最大流。)
平衡分割问题可以表述为:给定一个包含n个顶点的图和预算b,平衡分割将所有的顶点分成两个集合S和T,使得 ,并且S和T之间最多有b条边。
Integer linear programming (ILP,整数线性规划)

3D匹配
在3D匹配问题中,除了n个男孩和n个女孩,新增了n个宠物;它们之间的相容关系被表达为一个三元组的集合,集合中每个元素都包含一个男孩、一个女孩和一个宠物。直观上,三元组(b,g,p)意味着男孩b,女孩g和宠物p能够融洽相处。我们需要求n个独立的三元组,从而最终形成n个和谐的“家庭组合”。
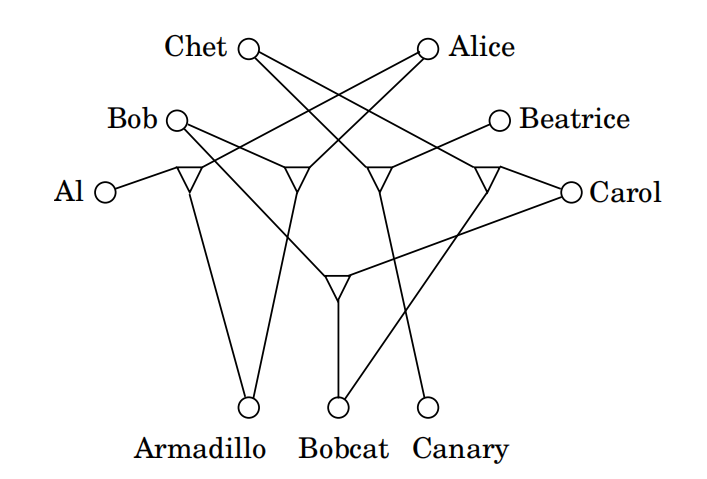
独立集、顶点覆盖和团
最长路径问题

背包问题和子集和


8.2 NP - 完全问题
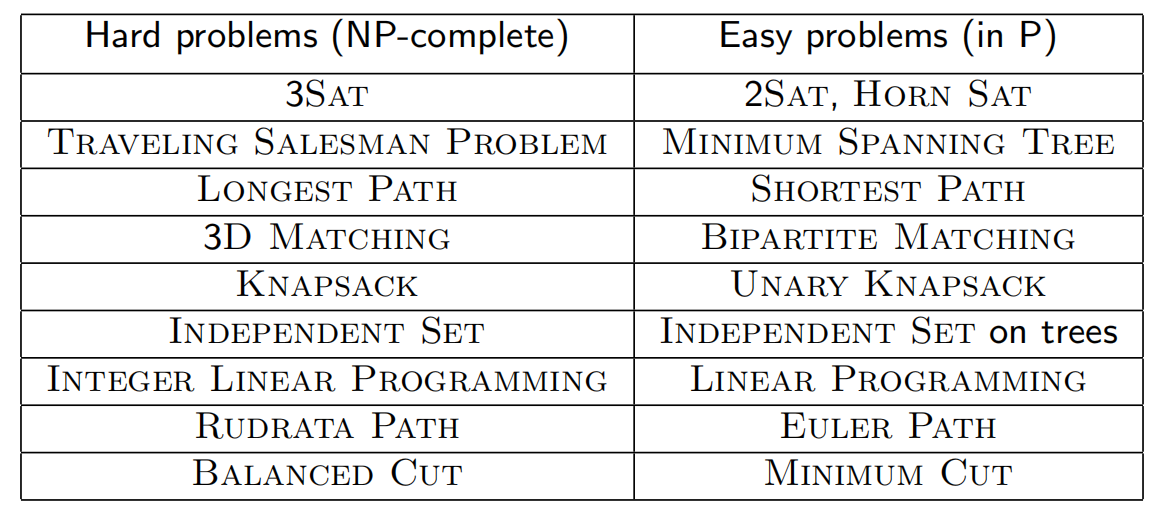
搜索问题定义是:任意可能解的正确性都能被快速检验,也即:存在以问题实例I(用于确定待求解问题的数据)和可能解S为输入的高效检验算法C,其输出为true的充要条件是S确实是 的解。此外,C(I,S)必须是关于实例长度 的多项式时间算法。我们将所有这些搜索问题称为NP-问题。
所有能在多项式时间内求解的搜索问题被记为P。也即,前述表右侧的问题都是属于P的。
: polynomial time,能在多项式时间内求解的搜索问题
: nondeterministic polynomial time,搜索问题,即任何可能解的正确性能在多项式时间内被验证
?
寻找证明问题:

属于搜索问题,因此属于NP类。因为数学陈述的形式证明可以通过高效的算法进行验证。
所以如果P= NP,那么将存在一种高效的方法来证明任何定理
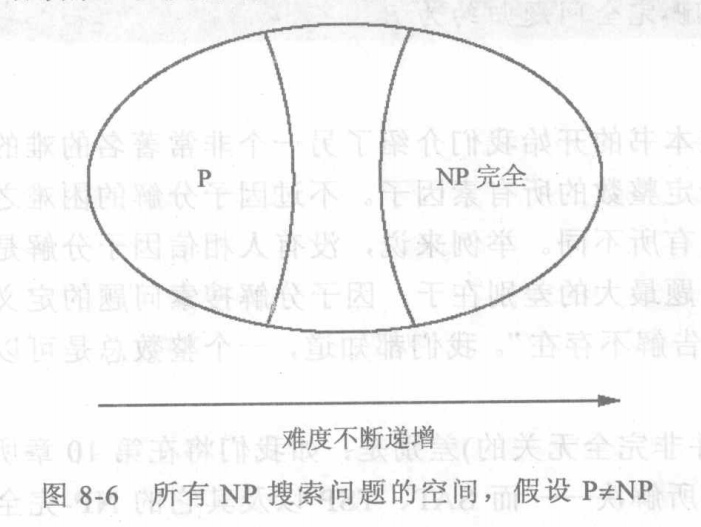
我们相信 ,而且我们还能说明关于表左侧的问题,已经证明都可以在某种意义下被归约为完全相同的问题。我们还将使用归约来说明这些问题是NP搜索问题中最难的——只要其中某一个存在多项式时间算法,则所有NP问题也都存在类似的算法。
再论归约:

,所以成立
归约的使用:

也可以写为
:称一个搜索问题是NP-完全的,是指其它所有搜索问题都可以归约到它。(注意,这样的问题是否存在并不知道)
因数分解:求给定整数的所有素因子。是搜索问题(),但是没有人相信是 .因为它与其他问题之间的差异在于:不存在我们所熟悉的句子“或者报告解不存在”,它一定是有解的。
8.3 所有的归约
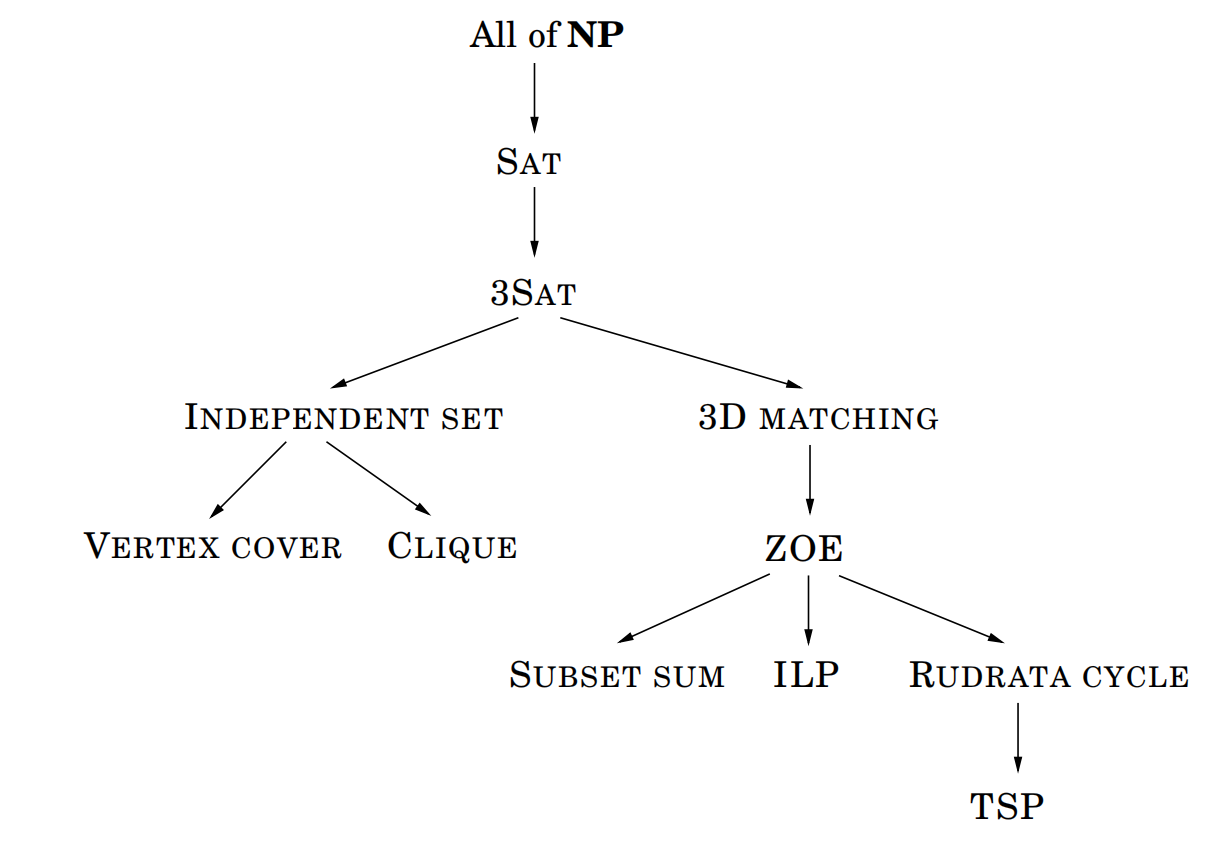
我们最终将得到这样一张图,图中所有的点都是 的。而且这些箭头其实是双向的,因为TSP既在 All of NP 里,也在图的最下面作为单独的节点。
Rudrata(s, t)-Path→Rudrata Cycle
Rudrata环路问题:给定一个图,求是否存在一个恰好经过每个顶点一次的环路?
Rudrata(s,t)-路径问题,需要指定两个特殊的顶点s和t,然后求一条由s到t的恰好经过每个顶点一次的路径。
现在我要做归约:
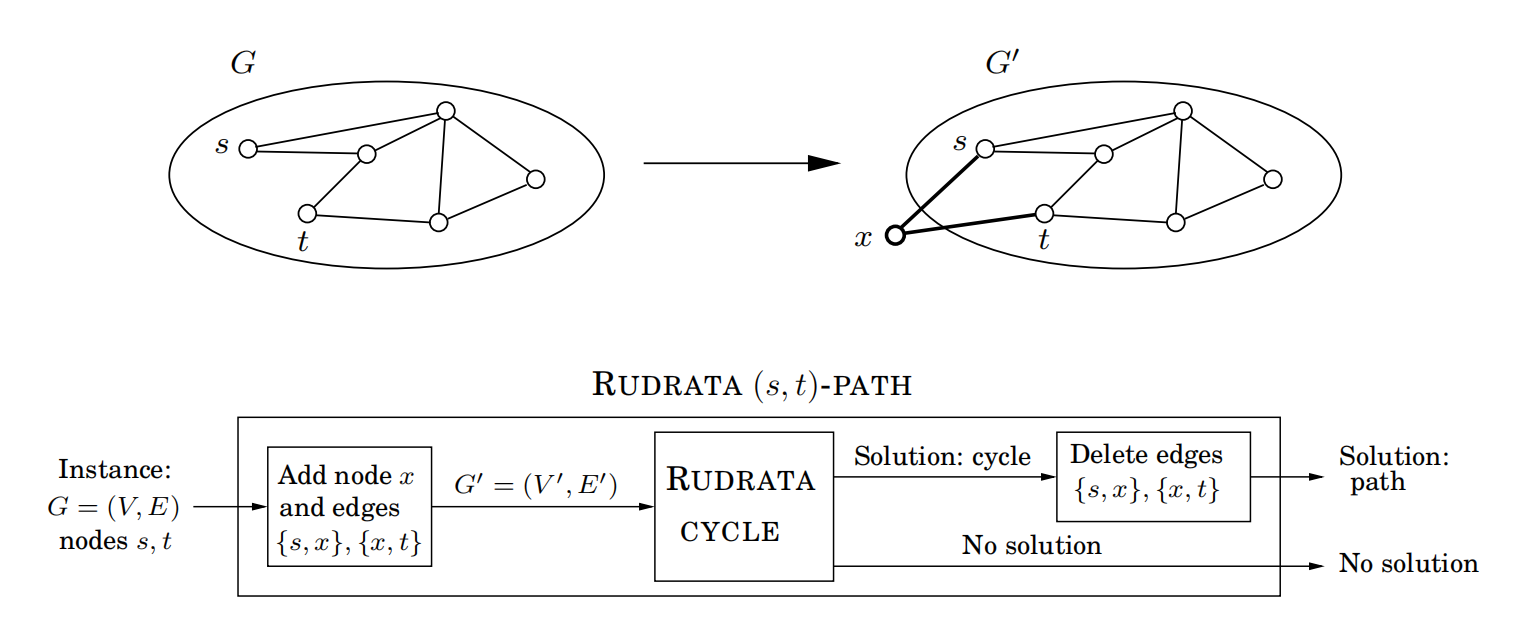
加点x是归约的f,删除点x是归约的h。这样我们就归约好了。
3SAT→Independent Set
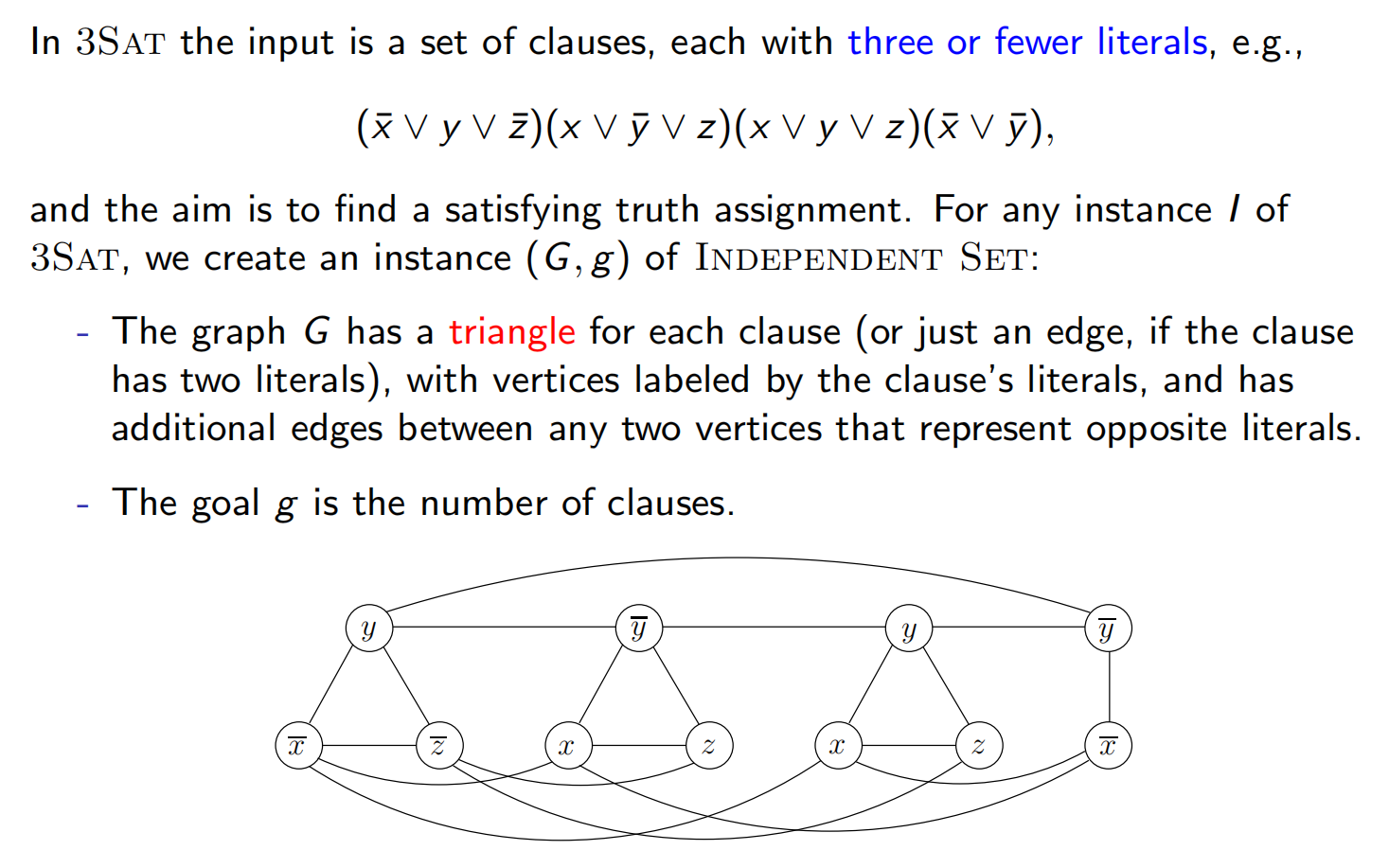
容易看出,多项式时间的f和h也是很容易构造的。(f如上图,h只需要从每个三角形中取一个true的,即可得到3SAT的答案)
SAT→3SAT

事实上,即使在3SAT中增加每个变量最多在不同子句中出现三次这一限制,其仍然是很难的。我们构造一个3SAT到这个特定版本的归约:
假设在3SAT的实例中,变量x在k>3个子句中出现。则将其第一次的出现替换为 ,第二次的替换为 ,如此继续,将其所有的k次出现都替换为一个新的变量。接下来,增加一组子句
在新的公式中不再存在出现次数超过3的变量(事实上,已没有出现超过两次的文字)。同时,上面的附加子句使得这些变量都必须取值相同。因此原3SAT实例可满足当且仅当加入限制后的实例可满足。
Independent Set→Vertex Cover
只需要注意一点:节点集合S是图G=(V,E)的一个顶点覆盖,当且仅当剩余节点的集合V-S是G中的一个独立集
因此,为了求解独立集问题的一个实例 ,仅需找到 的一个包含 个节点的顶点覆盖。如果存在这样的顶点覆盖,则选择所有未包含在其中的节点即可构成一个独立集。如果不存在这样的顶点覆盖,则G不可能有一个规模为g的独立集。
Independent Set→Clique
定义补图:原来的图中有边的没边,没边的加边得到 。于是节点集S是G的一个独立集当且仅当S是 中的一个团。
3SAT→3D Matching
首先,我们构造一个“器件”:考虑如下四个三元组的集合,我们将每个三元组表示为一个三角形节点,三个角分别连接了一个男孩、一个女孩和一个宠物。
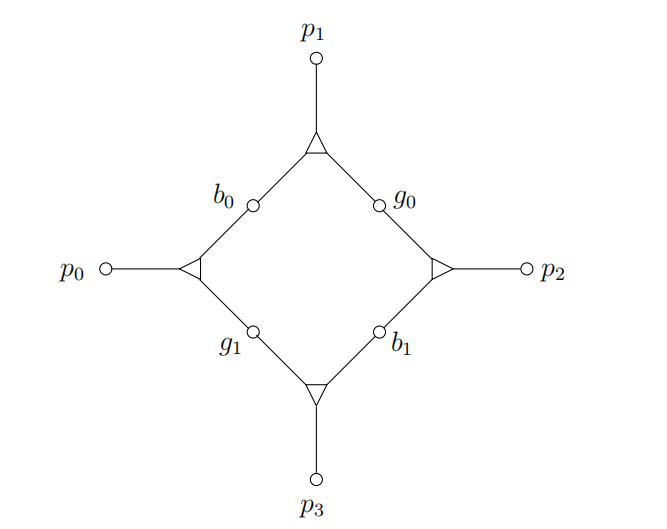
假设男孩、以及女孩、不属于任何其它的三元组。为了把这两个男孩两个女孩匹配起来,任意的匹配要么包含两个三元组和,要么包含和。因此,以上的“器件”就具有了两个可能的状态,恰好类似于一个典型的布尔变量的行为。对于每个3SAT的变量都生成一个上面的器件,用下标x标识: , ,
这样,我们就对于每个变量赋予了意义:若 ,则男孩 与女孩 相匹配,否则与 相匹配。
然后,对于每个字句,构造一个男孩一个女孩,并且使用每个变量所对应的器件(注意到由于器件能够有true false的意义是由于我们让 , 不与外部相连。所以我们在构造字句所对应的3D匹配的时候实际上是用每一个器件中的宠物作为接口来实现的)来做一个3SAT→3D Matching的对应。
例如子句:
引进男孩: 和女孩: 这些三元组中的宠物将用于反映这些子句被满足的三种途径:(1),(2),(3)。 这三个途径只要有一个走得通就行了。
对于(1),我们构造三元组来对应:,其中即的器件中的宠物。
以下是为什么选择的理由:若,则与匹配且与匹配,因此用掉了宠物和。在此情况下,和可以和相匹配。但如果,则和将被采用,于是和就无法采用这种方式进行匹配了。
所以这个三元组就对应了c成立与否的一条途径。而对于每个字句中的变量都构造这样一个三元组,那么可以发现,c成立等价于 顺利被匹配掉了。
我们需要确定一点,即对于一个文字在子句中的每次出现,都有不同的宠物与和相匹配。这其实很简单:由此前的一个归约,我们可以假定每个文字的出现都不会超过两次,因此每个变量的器件都有足够多的宠物,其中两个对应于否定的出现,另两个对应于非否定的。
归约到此似乎已经完成了:通过简单地查看每个变量的器件中哪个女孩被匹配,我们可以从任意的匹配中恢复出一个可满足赋值。并且,由任意的可满足赋值我们可以对与每个变量对应的器件进行匹配,使得如果则选择三元组和,如果则选择和;并且每个子句将使得和与其所包含的一个满足文字对应的宠物相匹配。
还存在最后一个问题:在上一段最后定义的匹配中,有些宠物可能被剩余下来无从匹配。事实上,如果有个变量和个子句,则恰好有个宠物将不会被匹配(您可以检验该值一定为正的,因为每个变量最多有三次出现,且每个子句中最少有两个文字)。要解决该问题其实很容易:增加对新的男孩和女孩(两者已配对好了),假设这些新加入的孩子都是些“大众宠物情人”,只需将他们与所有剩下的宠物配对即可。
3D Matching→ZOE(Zero One Equations)
ZOE:

举例来说,使用ZOE的语言,我们可以这样表达3D匹配问题(个男孩、个女孩、个宠物和个男孩-女孩-宠物三元组)。对每个三元组,我们设置一个0 - 1变量,意味着第个三元组被用于匹配,反之则表示没有被使用。 现在我们要做的是写下一些方程以说明由所表达的解是一个合法的匹配。对每个男孩(或者女孩,或者宠物),假设包含他(她、它)的三元组下标为,于是对应的方程就是
其含义为恰好有一个三元组被包含在匹配中。例如,以下矩阵对应于我们此前看到的3D匹配实例:
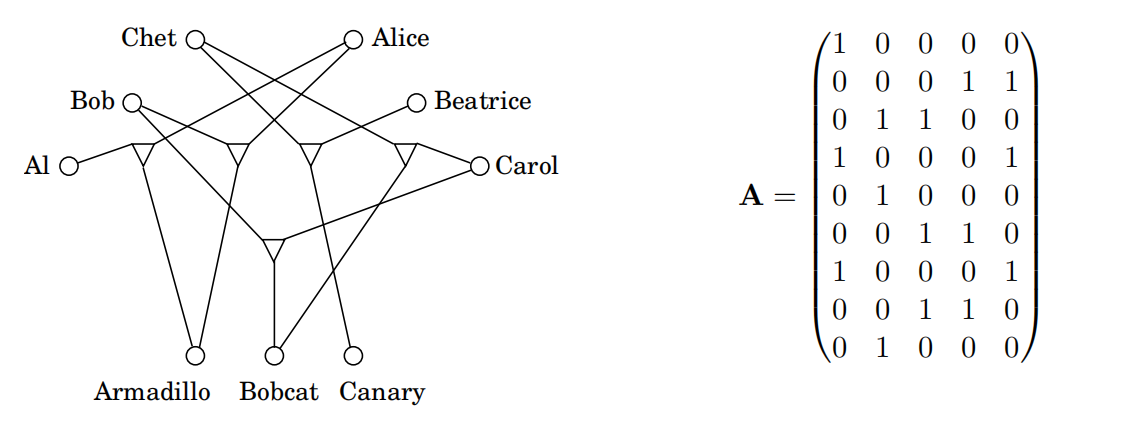
9行代表9个人(或宠物),每列代表一个三元组。
ZOE→Subset Sum
子集和问题:有一个集合,找一个子集,其和为一个给定的数。
ZOE转化为子集和:对每一列,其值为二进制编码(从上到下读)。找一些列,其和为11…1.这就是一个子集和问题了。
一个小问题:可能因为进位而导致非预期的成立,如:

不以2base,以n+1base,则不会进位了。
Special cases
3SAT是SAT的一个特例。3SAT的实例也都是SAT的实例,且对于两个问题其解的定义完全相同(即满足所有子句的赋值)。因此,存在可以由3SAT迁移到 SAT的赋值,归约中的函数f和h都是恒等函数。
ZOE→ILP
ZOE其实就是ILP的一个special case。讲把ZOE的每个等式重写为两个不等式,把 改写为两个约束 和 即可。
ZOE→Rudrata Cycle
Rudrata Cycle:求图中的一个环路,使其恰好经过每个顶点一次。
证明其为NP-完全的需要分为两步:
- 首先我们将ZOE归约为Rudrata环路的一个推广问题,所谓含有成对边的Rudrata环路(RUDRATA CYCLE WITH PAIRED EDGES)问题
- 然后我们去除它的附加特征,将其归约为一个普通的Rudrata环路问题。
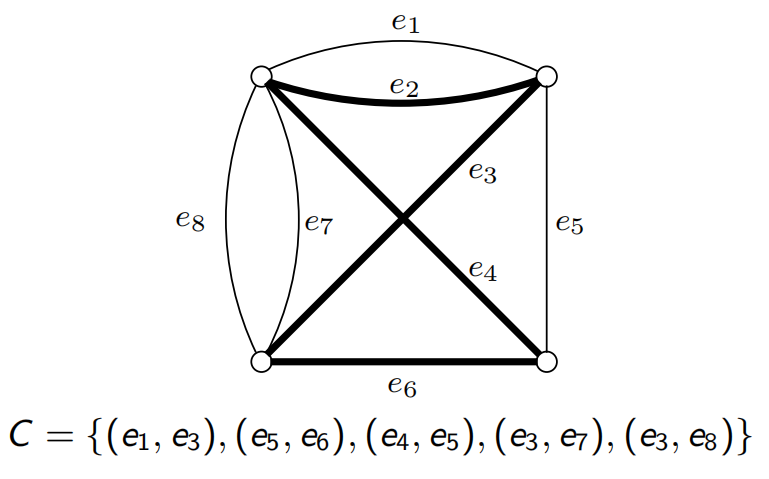
含有成对边的Rudrata环路(注意这里的成对边的意思不是要起终点一样!):
给定一个图 和一个边对集合 。我们要求一个满足以下条件的环:(1)经过所有的顶点一次 (2)对C中的每个边对 ,环路恰好使用了其中的一条边——要么 ,要么 。
下面我们对每个ZOE实例来构造一个含有成对边的Rudrata环路:
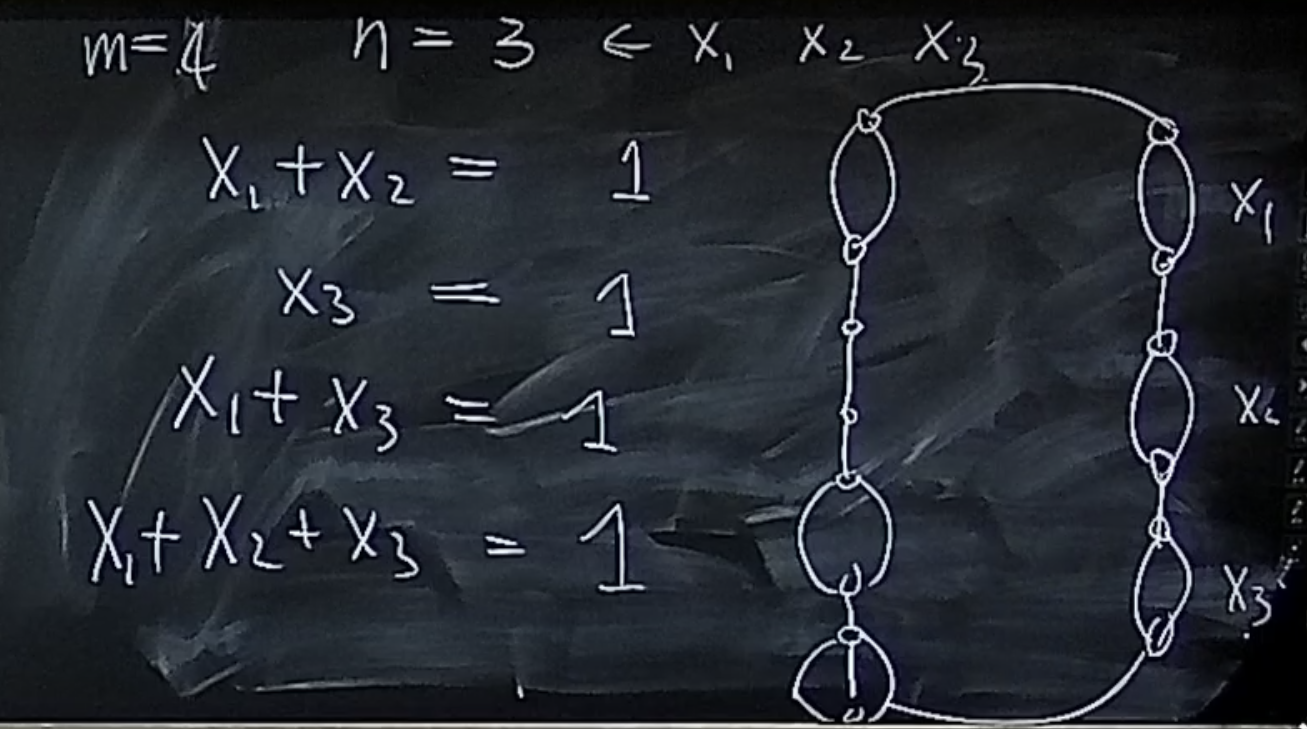
左边的equations:多条边中选一条走,表示这一个变元赋1,其他的赋0,
右边的variables:每个变元对应两条,一条表示赋1,一条表示赋0
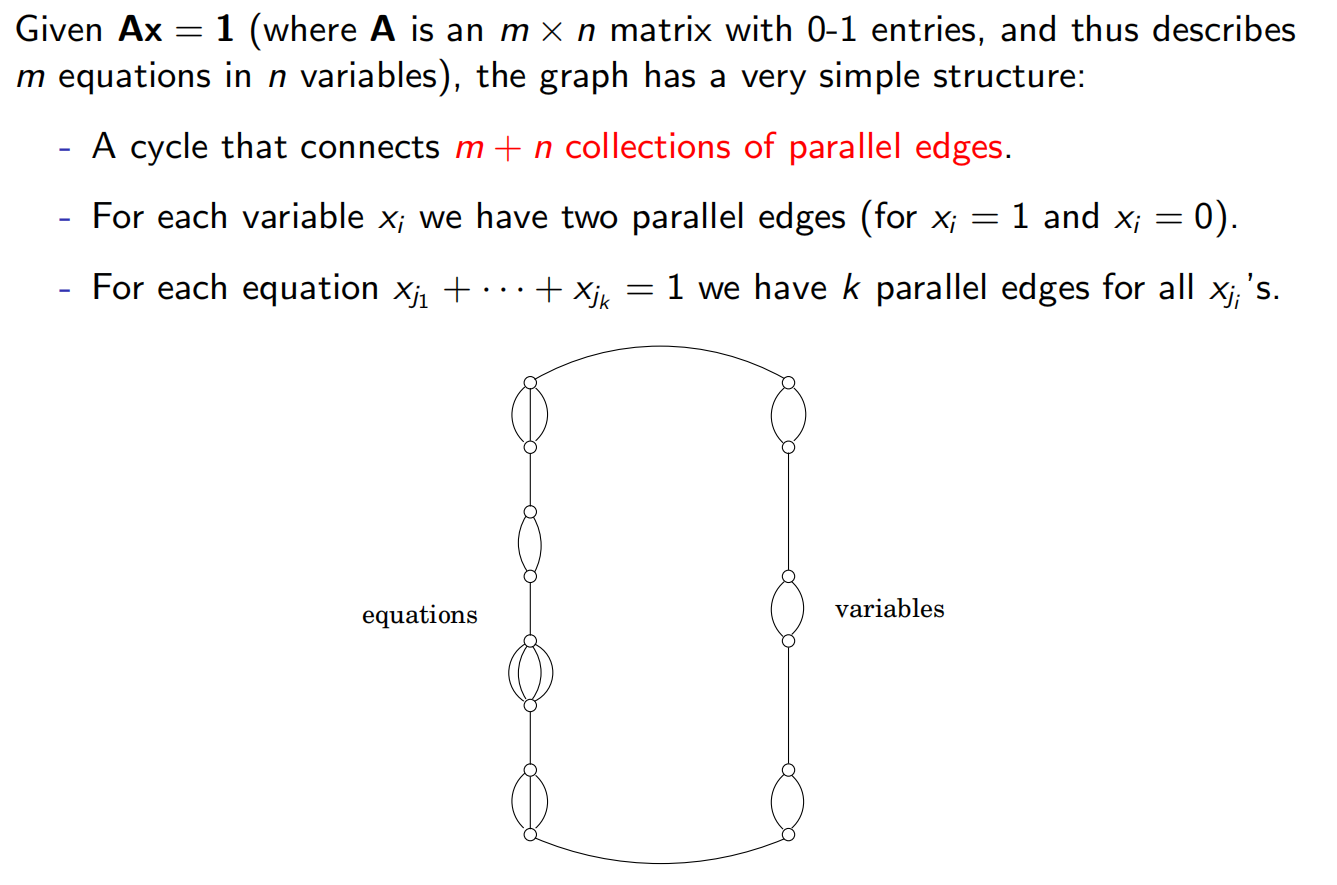
当然,整个归约不可能如此简单。环路应该恰好从每个边对中选择一条边。而现在我们还剩下一个可用的信息:边对集合C。对于每个方程(共m个)和其中的所有变量x,我们在C中加入如下的边对(e,e’),其中e是与x;在特定方程中的出现对应的边(左侧),e’是x=0对应的边(图的右侧)。
去除边对:引入这样一个结构,这样对于每个成对边,我们加入了中间的12个点,为了走所有的点,我们就实现了只能走其中一条边。
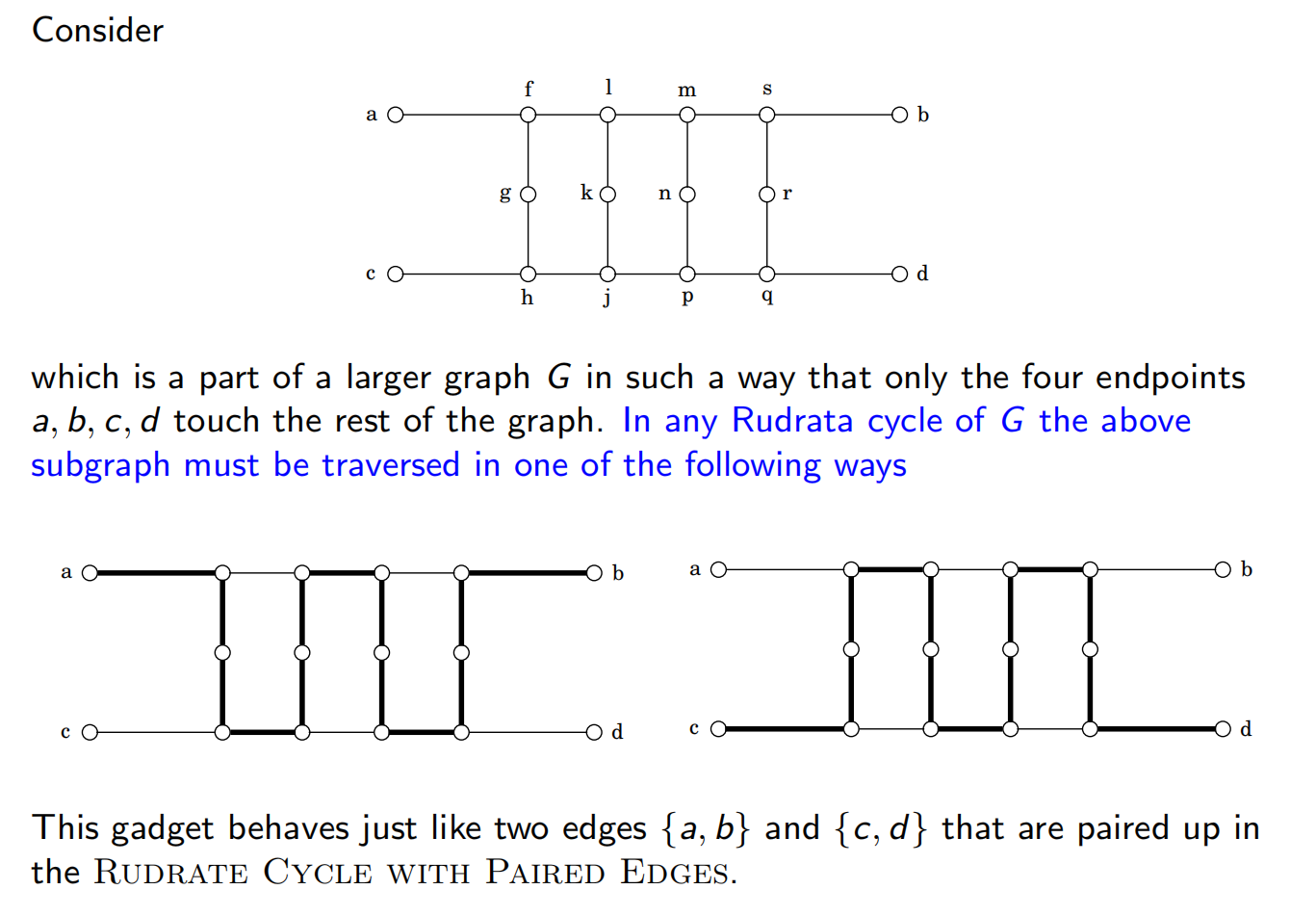
这样图就变成了:
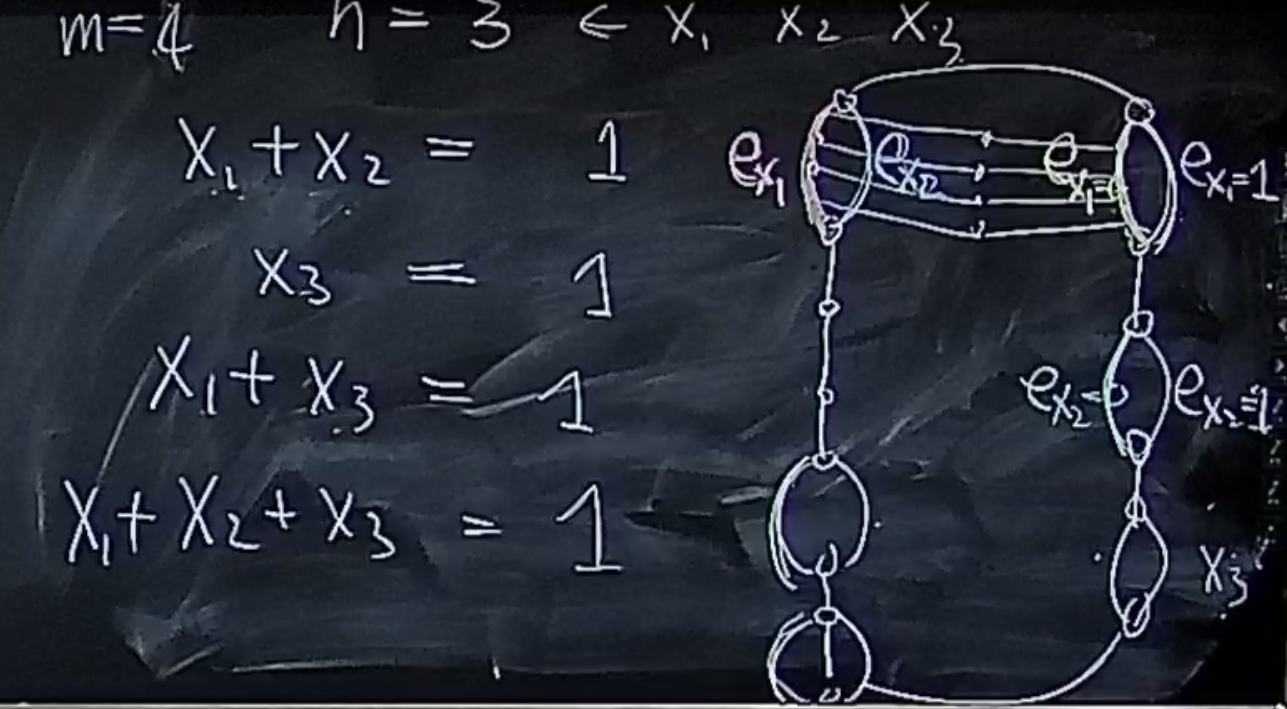
对于两个pair指向一条边怎么办?左边的两个equ都用到了 , 会与右边的同一条边相连?稍作修改:
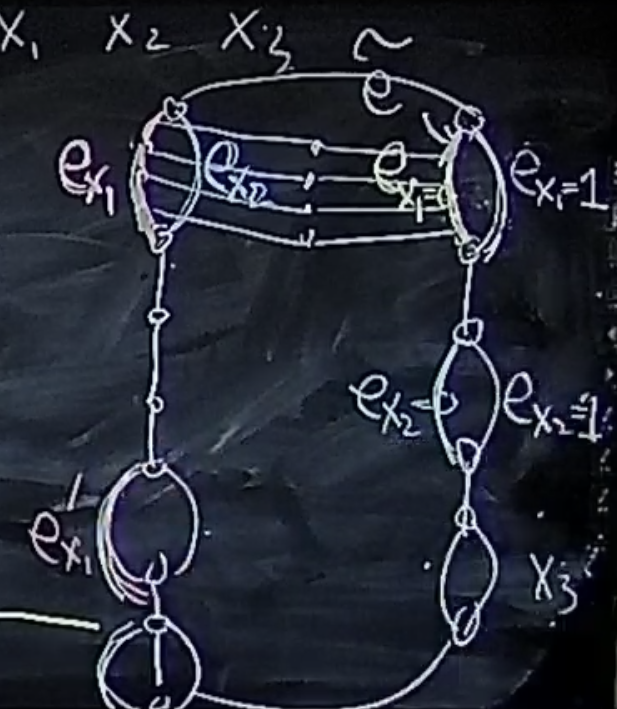
用划分之后的上面的一小段来代替原来的边,这样就解决了。
归约到此结束。
Rudrata Cycle → TSP
给定一个图G=(V,E),构造如下的 TSP实例:城市集合等同于 V,如果{u,v}为G中的一条边,则令城市u和v间的距离为1,否则为 ,其中 待定。TSP实例的预算等于节点数量 。
如果G有一个Rudrata环路,则该环路同样也是TSP实例在预算内的一条旅行路线。反之,如果G没有Rudrata环路,则无解:最经济的TSP路线代价至少为 。如此就将Rudrata环路归约到了TSP。
通过调整 的值,可以得到两个有趣的结果:如果 ,即所有的距离要么为1要么为2,则所有的距离值满足三角不等式,即:若i,j,k为城市,则 (证明:对于任意 ,都有 )。这是TSP的一个非常具有实用价值的特例,而且也是一个相对简单的情形。在第9章中我们将看到,该情形是可以被高效地近似求解的。
另一方面,如果 是一个很大的数,则最终的TSP将不再满足三角不等式,但却具有另一个重要的性质:要么其有代价不超过n的解,要么其所有解的代价至少为 (此时可以为任意大于 n的数)。除两者之外没有其它可能!如我们在第9章中将看到的,这一重要的跨度意味着,除非P=NP,否则该情形将不存在任何近似算法。
任意NP问题→SAT
现在我们将完成整个归约的循环,指出所有这些问题—事实上是所有的 问题都可以归约为 。
特别地,我们将首先说明所有 问题都可以归约为 的一个推广:所谓的电路可满足性问题(CIRCUIT SAT,简称电路 SAT)。推广在哪儿?电路SAT有已知的输入门。
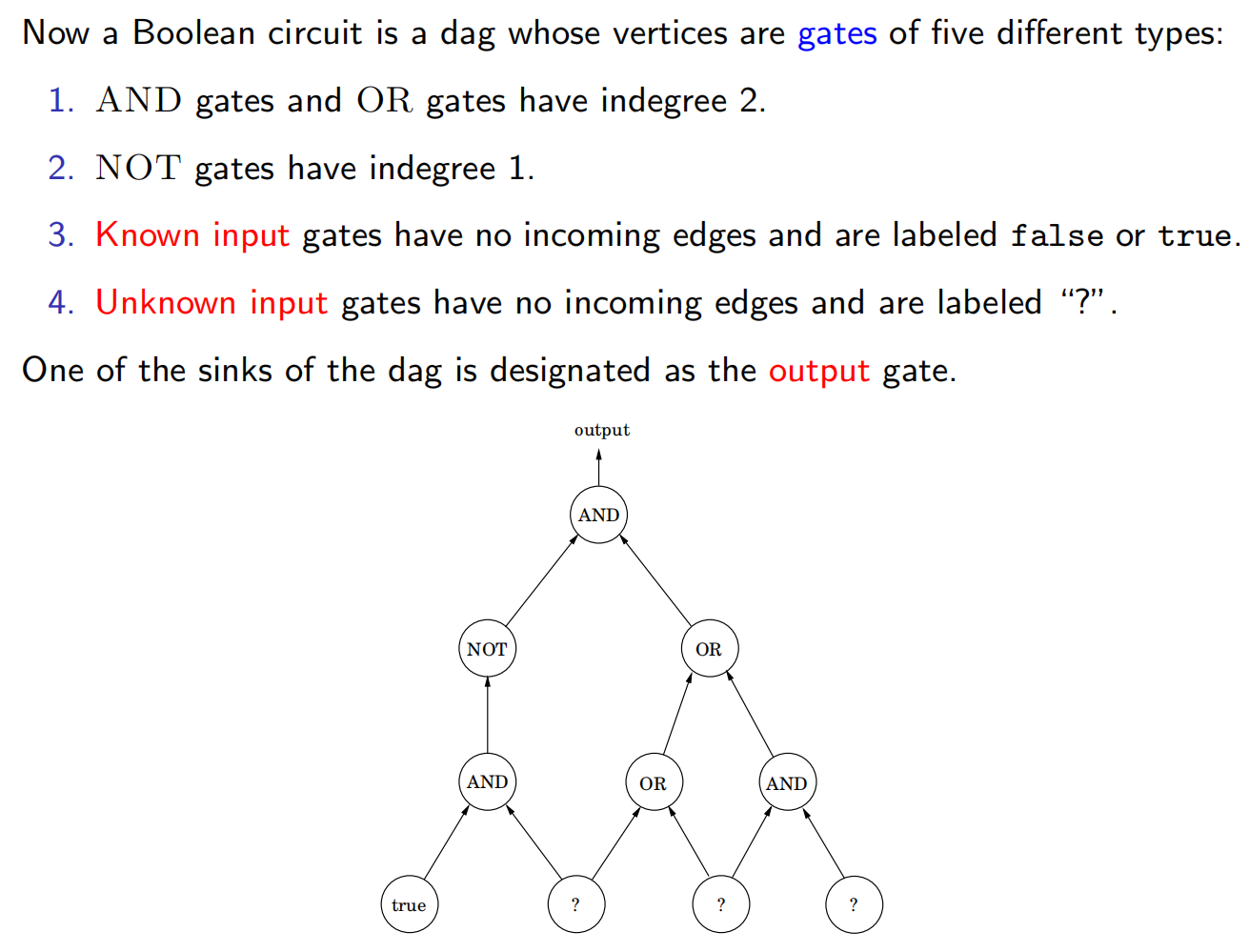
电路 SAT是如下的搜索问题:给定一个电路,求其中未知输入的一个可满足赋值,使得输出门上的值为 true,或者报告这样的赋值不存在。
Circuit SAT → SAT:
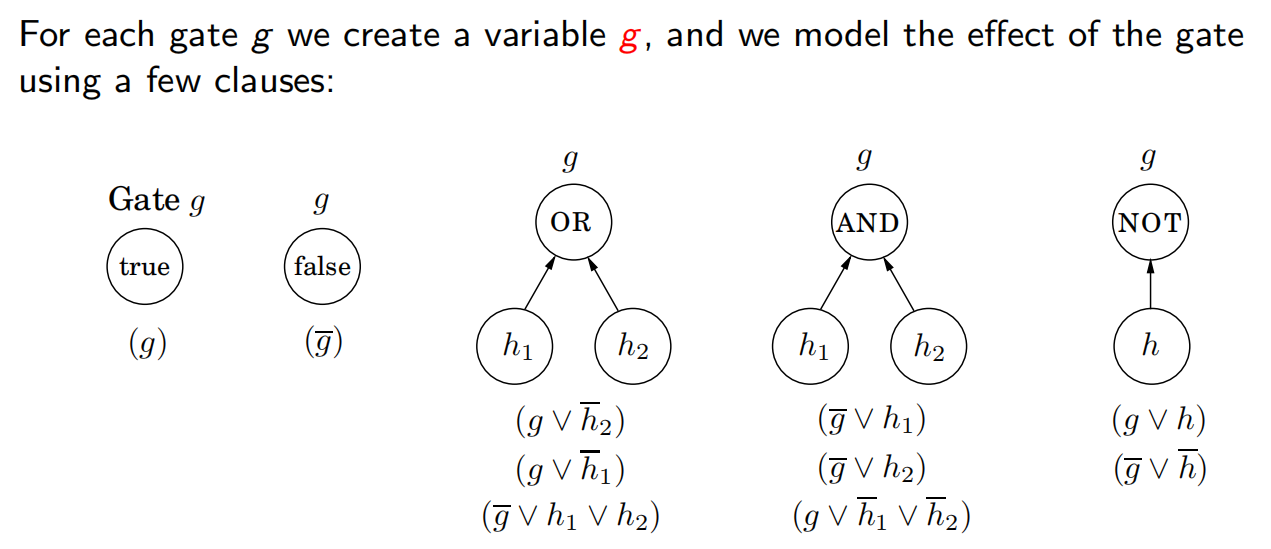
Any problem in NP → Circuit SAT (informal)
假设 是一个 问题。我们必须找到由 到 的一个归约。这看起来很困难,因为我们对 几乎还一无所知!
关于 ,我们所知的全部就是它是一个搜索问题,我们必须利用这一点。搜索问题的主要特征是其任意解都能被快速检验,即:存在算法 ,以问题实例 和可能解 为输入,判断 是否为 的解。此外, 做出判断的时间关于 的长度(我们可以假设 本身是用二进制串表示的,且我们知道该串的长度关于 的长度是多项式规模的)为多项式规模的。
回顾7.7节的结论,任意多项式算法都可以被表示为一个电路,其输入门将用于编码算法的输入。对任意长度(输入的比特数)的输入,电路可以扩展出适当数量的输入门,但电路中门的总数关于输入数量是多项式规模的。如果问题的多项式时间算法给出的是一个是或否的答案(类似如下情形的 :“S所编码信息的是否为I所编码实例的解?” ),则该答案将由输出门给出。
总结一下,给定问题 的一个实例 ,我们可以在多项式时间内构造一个电路,其已知输入为 对应的比特,未知输入为 对应的比特,则其最终输出为true当且仅当未知输入对应的 为 的解。换句话说,电路未知输入的可满足赋值与 的实例 的解是一一对应的。归约到此结束。
后记
非常感谢陈翌佳老师两个学期以来讲解的线性代数和算法课程。能在进入大学的前两个学期上到陈老师的课真的无比荣幸。陈Sir的授课从头到尾都保持着极高的水准,对授课内容有自己的看法与见解并且深入浅出。无论是Slides的制作,讲课的节奏调整,对于同学们提问事无巨细的回答,还是作业出的高质量的题目,都让人受益匪浅。
下面的章节限于时间因素无法讲解,但所有内容都可以在书中查阅,故将目录列在这里,如有具体需要可以查阅教材。

